Le Théorème de Gödel

Le Théorème de Gödel

Kurt Gödel (1906-1978) est un logicien et mathématicien austro-américain. On connaît surtout de lui deux théorèmes dits d’incomplétude en logique mathématique. Mais on lui doit aussi des travaux en relativité générale, notamment sa fameuse solution des équations d’Einstein décrivant un univers en rotation.
Gödel est né en 1906 à Brno. Il étudie à Vienne à partir de 1924 et établit son théorème d’incomplétude en 1930, pour le publier en 1931. Il émigre aux Etats-Unis en 1940 et occupe un poste à l’Institute for Advanced Studies. Cet emploi lui laisse beaucoup de temps de libre, et à côté de ses travaux de logique, il se consacre beaucoup à la philosophie.
Jusqu'au début du siècle les mathématiciens étaient persuadés qu'on pouvait, un peu à la manière des écoliers en géométrie, démontrer toutes les vérités mathématiques par déduction.
Gödel a démontré en 1931 deux résultats mathématiques :
=> Il se peut que dans certains cas, on puisse démontrer une chose et son contraire (inconsistance).
=> Il existe des vérités mathématiques qu’il est impossible de démontrer (incomplétude)
Le plus célèbre de ces résultats est le second, qu’on appelle théorème d’incomplétude de Gödel.
Les théorèmes d’incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931. On se posait alors la question de savoir si les systèmes axiomatiques proposés pour démontrer toutes les théories mathématiques connues pouvaient démontrer leur propre consistance logique. En gros, pouvait-on être sûr que l’on n’aurait jamais des démonstrations contradictoires d’un énoncé de mathématique déduit d’un des systèmes d’axiomes censés fonder les mathématiques ?
GÖDEL s’attaque à la démonstration de la cohérence de l’analyse, à l’aide de moyens
finis. Son idée est de démontrer la cohérence relative de l’analyse, et de l’arithmétique, cette dernière étant de démonstration plus aisée.
• Il s’ appuiera à cette fin sur l’axiomatique de PEANO. Le projet évoluera en suite, et GÖDEL
va finalement décider de prouver que la démontrabilité et la non contradiction
peuvent, même indirectement, être exprimées dans le langage objet de la
théorie, sans que cela entraîne des contradictions fatales
Peut-on tout démontrer en mathématiques ?
Quand on fait des mathématiques, on manipule des énoncés.
Un énoncé est une suite de symboles ou une phrase ayant un sens mathématique précis.
Par exemple 2 + 2 = 4 ou « Il existe une infinité de nombres premiers » sont des énoncés mathématiques.
Un énoncé mathématique est soit vrai, soit faux : par exemple 2 + 2 = 5 est un énoncé faux.
Quand on considère un énoncé mathématique, on ne sait pas forcément à l’avance s’il est vrai ou faux.
Le travail du mathématicien, c’est justement d’essayer de savoir lesquels sont vrais et lesquels sont faux. Et pour cela, il utilise un outil : il fait des démonstrations.
Si un mathématicien arrive à démontrer un énoncé, on considère que cet énoncé est « vrai ».
S’il démontre le contraire, alors on dit que l’énoncé est faux.
Les mathématiques reposent donc sur l’idée que si un énoncé est vrai, alors il doit en exister une démonstration, et il n’y a plus qu’à la trouver. Mais est-on sûr que tout ce qui est « vrai » est forcément « démontrable » ? Se pourrait-il qu’il existe des choses vraies mais indémontrable ?
Le grand mathématicien David Hilbert,
Les conceptions scientifiques de David Hilbert ont une grande influence sur les mathématiciens de son époque.

Hilbert s’oppose fermement au pessimisme scientifique prôné en particulier par le physiologiste Emil du Bois-Reymond, pour qui il est des questions en sciences qui resteront toujours sans réponse, une doctrine connue sous le nom d’« Ignorabimus » (du latin ignoramus et ignorabimus : « Nous ne savons pas et nous ne saurons jamais »). Hilbert, pour qui « il n’y a pas d’Ignorabimus en sciences naturelles », propose, au contraire, dans une allocution de 1930, de s’appuyer sur un slogan resté célèbre : « Nous devons savoir, nous saurons » (Wir müssen wissen. Wir werden wissen).

La découverte de paradoxes dans les théories proposées par Cantor et Frege sur les fondements des mathématiques ébranle la confiance en ceux-ci. Certes, on a de nouvelles théories des ensembles qui sont exemptes des paradoxes connus, mais comment s’assurer qu’on n’en trouverait pas de nouveaux ?
L'intuitionnisme est une philosophie des mathématiques que L. E. J. Brouwer a élaborée au début du xxesiècle.

Pour Brouwer, les mathématiques sont une libre création de l'esprit humain et tous les objets qu'elles manipulent doivent être accessibles à l'intuition. L'intuitionnisme a pour conséquence une profonde remise en cause des mathématiques, notamment en refusant l'infini actuel : un nombre réel ne peut être représenté comme une suite infinie de décimales qu'à la condition de disposer d'un moyen effectif de calculer chacune de ces décimales ; on parle alors de réel constructif. Sur le plan logique l'intuitionnisme n'accepte pas le raisonnement par l'absurde ou le tiers exclu pour la raison que ces principes permettent de démontrer des propriétés de façon non constructive : par exemple si on veut démontrer l'existence d'un nombre réel satisfaisant une certaine propriété, on peut raisonner par l'absurde, supposer qu'un tel réel n'existe pas, en déduire une contradiction et conclure que donc un tel réel existe, mais cette démonstration ne donne aucune indication sur la façon dont on pourrait calculer ce réel. Pour un intuitionniste on a juste démontré que l'existence d'un tel réel n'est pas contradictoire, mais pas que ce réel existe. La caractéristique distinctive fondamentale de l’intuitionnisme est son interprétation de ce que signifie « être vrai » pour une affirmation mathématique. Dans l'intuitionnisme originel de Brouwer, la vérité d'une affirmation mathématique est une affirmation subjective: une affirmation mathématique correspond à une construction mentale, et un mathématicien ne peut affirmer la vérité d'une affirmation qu'en vérifiant la validité de cette construction par intuition. L'imprécision de la notion intuitionniste de vérité conduit souvent à des interprétations erronées de sa signification. Pour un intuitionniste, l'affirmation selon laquelle un objet possédant certaines propriétés existe est une affirmation qu'un objet possédant ces propriétés peut être construit. Tout objet mathématique est considéré comme le produit d'une construction d'un esprit, et donc l'existence d'un objet équivaut à la possibilité de sa construction. Cela contraste avec l'approche classique pour laquelle l'existence d'une entité peut être prouvée en réfutant sa non-existence. Pour l'intuitionniste, ce n'est pas valable; la réfutation de l'inexistence ne signifie pas qu'il soit possible de trouver une construction pour l'objet putatif, comme cela est nécessaire pour affirmer son existence. En tant que tel, l’intuitionnisme est une forme de constructivisme mathématique, mais ce n'est pas la seule.

L’hôtel de Hilbert.(d'après JEAN-PAUL DELAHAYE MATHÉMATICIEN INFORMATICIEN) Cette expérience de pensée est généralement attribuée au mathématicien David Hilbert (1862 - 1943)L'hôtel de Hilbert, ou hôtel infini de Hilbert, illustre une propriété paradoxale des ensembles infinis en mathématique, qui est que, contrairement à ce qui se passe pour les ensembles finis, une partie stricte peut avoir autant d'éléments que le tout.
Supposons qu'un hôtel (fictif) possède un nombre infini de chambres, numérotées par nombre entier à partir de 1, et toutes occupées.
Malgré cela, l'hôtelier peut toujours accueillir un nouveau client.
Arrive un client. « Pas de problème, lui répond l'hôtelier. Installez-vous dans la chambre 0. Je demande au client de la chambre 0 de passer dans la chambre 1, à celui de la chambre 1 de passer dans la chambre 2, etc. »
L'accueil dispose bien sûr d'un téléphone spécial qui permet de téléphoner simultanément à toutes les chambres en demandant au client de la chambre n de passer en n+1.
Le nouveau client a pu être reçu.
Dix minutes plus tard arrive un car (infini, bien sûr) de nouveaux clients qui demandent à passer la nuit dans l'hôtel. « Pas de problème », répond l'hôtelier au chauffeur du car, et il utilise son téléphone pour demander au client de la chambre n de passer dans la chambre 2n. Il indique alors au chauffeur du car que le voyageur numéro i de son car peut disposer de la chambre 2i+1 (qui est effectivement libre, puisque toutes les chambres de numéro impair ont été libérées).
Une demi-heure plus tard arrive un groupe plus important constitué d'une infinité de cars, chacun ayant à leur bord une infinité de passagers. « Pas de problème, je vous arrange ça », répond l'hôtelier. Il téléphone au client de la chambre i de passer dans la chambre 2i+1 (ce qui libère toutes les chambres ayant un numéro pair) et donne la consigne suivante au responsable du groupe d'autocars : le passager numéro i du bus j doit occuper la chambre 2i+1(2j+1).
Tout se passe bien, et jamais deux voyageurs différents ne se sont vu attribuer la même chambre.

Hilbert s’oppose également violemment à l’intuitionnisme du mathématicien néerlandais Brouwer, que promeut ce dernier pour résoudre la crise des fondements, et qui est une remise en cause radicale de ceux-ci.
Le programme de Hilbert
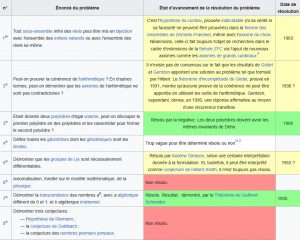
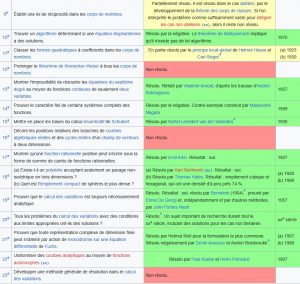
Pour régler la question des fondements, Hilbert conçoit un programme dont il établit les prémisses en 1900 dans l’introduction à sa célèbre liste de problèmes, le second problème étant celui de la cohérence de l’arithmétique.
Lors du deuxième congrès international des mathématiciens, tenu à Paris en août 1900, David Hilbert entendait rivaliser avec le maître des mathématiques françaises, Henri Poincaré, et prouver qu’il était de la même étoffe.
Il présenta une liste de problèmes qui tenaient jusqu’alors les mathématiciens en échec. Ces problèmes devaient, selon Hilbert, marquer le cours des mathématiques du xxe siècle, et l’on peut dire aujourd’hui que cela a été grandement le cas.
Publiée après la tenue du congrès, la liste définitive comprenait 23 problèmes, aujourd’hui appelés les problèmes de Hilbert.
Il développe ensuite ce programme dans les années 1920, avec ses collaborateurs.
Tant que l’on manipule le fini, les mathématiques sont sûres.
L’arithmétique élémentaire (en un sens qui doit se préciser) est sûre. Pour justifier l’utilisation d’objets abstraits ou idéaux, en particulier infinis, il suffit de montrer que la théorie qui les utilise est cohérente, mais bien sûr cette cohérence doit elle-même être démontrée par des moyens finitaires.
On peut alors affirmer l’existence de ces objets. Cette approche est ce que l’on a appelé le « formalisme ».
Le théorème de complétude, démontré par Kurt Gödel dans sa thèse en 1929, indique sommairement que l’on ne pourra trouver de nouveaux principes de raisonnement purement logiques autres que ceux déjà connus. Cela semble aller dans le sens de Hilbert. D’autres résultats qu’Hilbert obtient avec Wilhelm Ackermann dans les mêmes années semblent aller également dans ce sens.
Mais, même si Hilbert n’a pas explicitement formalisé le système des mathématiques finitaires, on considère généralement qu’il s’agissait d’une théorie arithmétique, sans préciser plus avant, une théorie qui satisfaisait les conditions des deux théorèmes d’incomplétude que Gödel expose en 1930 et publie en 1931, théorèmes devenus célèbres depuis.
Le second théorème d’incomplétude montre que l’on ne peut pas prouver dans cette théorie sa propre cohérence, et donc certainement pas celle de théories plus fortes qui assureraient la fondation des mathématiques.
C’est donc l’échec du programme de Hilbert. Il est d’ailleurs probable que Gödel, motivé par le programme de Hilbert, avait tout d’abord voulu prouver la cohérence de l’arithmétique.
Gödel mit donc fin à cet espoir en démontrant que tout système axiomatique permettant de faire de l’arithmétique devait contenir des propositions qui ne pouvaient être démontées, ou réfutées, en utilisant le système axiomatique en question.
Si l’on décidait qu’une de ces propositions était un autre axiome, on aurait un nouveau système, mais qui contiendrait lui aussi des propositions dont la vérité ou la fausseté sont indécidables.
Paradoxalement, on sait que certaines de ces propositions indécidables sont vraies, mais on ne peut le démontrer.
C’est souvent en ces termes que l’on parle « du » théorème d’incomplétude de Gödel, mais il s’agit en fait de son premier théorème d’incomplétude.
Le second théorème, lui, affirme que dans un système axiomatique donné permettant de faire de l’arithmétique, la proposition concernant la non-contradiction de ce système (c’est-à-dire le fait qu’on ne pourra jamais en déduire deux propositions mathématiques contradictoires) est elle-même indécidable.
Modèles et théories(d’après D. Kuperbe)
La notion de « vrai » était considérée comme quelque chose comme un attribut d’ universel et d’intrinsèque à un objet . En fait la notion de « vrai »est relative à ce qu’on appelle un « modèle ». Pour l’arithmétique, il n’y a pas trop de débat sur quel est le modèle. Mais par exemple pour la géométrie, il y a plusieurs choix ! Le modèle classique est celui de la géométrie euclidienne.
Pour trouver un système d’axiomes qui colle avec ce modèle, il faut prendre le 5ème axiome d’Euclide dans sa forme familière (une seule parallèle à une droite passe par un point donné extérieur à cette droite). Mais si vous changez de modèle, par exemple la géométrie riemannienne, il vous faut un autre système d’axiomes qui va bien, et que l’on peut obtenir en modifiant le 5ème axiome (aucune parallèle ne passe par un point donné extérieur à cette droite).


Donc si on choisit d’ajouter aux axiomes de Peano une proposition indécidable fausse, on obtient un système d’axiomes qui ne représente plus correctement l’arithmétique.
La définition axiomatique des entiers naturels de Peano peut être décrite par les cinq axiomes :
- L’élément appelé zéro et noté 0 est un entier naturel.
- Tout entier naturel n a un unique successeur, noté s(n) ou Sn qui est un entier naturel.
- Aucun entier naturel n’a 0 pour successeur.
- Deux entiers naturels ayant le même successeur sont égaux.
- Si un ensemble d’entiers naturels contient 0 et contient le successeur de chacun de ses éléments, alors cet ensemble est N.
Le premier axiome permet de poser que l’ensemble N des entiers naturels n’est pas vide, le troisième qu’il possède un premier élément et le cinquième qu’il vérifie le principe de récurrence.

Un théorème mathématique a ceci de remarquable que sa démonstration une fois établie vaut nécessairement et éternellement. Le théorème de Pythagore sera toujours vrai quelque soit le temps et le lieu. En ce sens, on peut bien y voir un modèle de raisonnement valide c’est-à-dire un idéal de vérité.
Toutefois quel usage peut-on faire de ce modèle hors du raisonnement mathématique comme tel ? La notion de modèle présuppose que les mathématiques puissent servir de norme ou de règle pour toute démonstration. Quel que soit l’objet du raisonnement, le modèle serait transférable et imitable.
Postulats et axiomes
Un axiome est quelque chose qui est considéré comme vrai mais sans preuve clairement définie. Vous savez juste que c’est vrai; tout le monde est d’accord avec cela, mais personne ne peut prouver qu’il a raison ou réfuter qu’il est incorrect. Dans une note plus formelle, la définition d’un axiome peut être donnée comme une proposition qui est évidemment vraie. Par exemple, le cinquième axiome d’Euclide, «Le tout est supérieur à la partie», est évident pour quiconque.
Un postulat est identique à un axiome, une proposition qui est évidemment vraie. La déclaration «Un segment de ligne droite peut être tracé reliant deux points quelconques» est le premier postulat du livre d’Euclide «Elements»..
Ce mot n’est plus utilisé en mathématique; il est plutôt remplacé par hypothèse ou conjecture. Il est toujours utilisé en physique théorique ou en philosophie.
Le cinquième postulat d’Euclide relatif aux droites parallèles est rebaptisé aujourd’hui: axiome d’Euclide ou axiome des parallèles.
La différence entre les termes axiome et postulat ne réside pas dans sa définition, mais dans sa perception et son interprétation. Un axiome est une affirmation commune et générale ayant une signification et un poids inférieurs. Un postulat est une déclaration plus significative et concerne un domaine spécifique. Puisqu'un axiome a plus de généralité, il est souvent utilisé dans de nombreux domaines scientifiques et connexes. Axiome est un terme archaïque (beaucoup) ancien, tandis que postulat est un nouveau terme en mathématiques..



La démonstration mathématique repose sur des principes ou des points de départ (postulats et axiomes) eux-mêmes indémontrables. L’argument repose sur une régression à l’infini : pour démontrer, il faut raisonner en partant de principes. Or si ces principes sont démontrables alors il faut les démontrer au moyen d’autres principes qui eux-mêmes doivent être démontrés et ce, à l’infini. Par conséquent, la démonstration doit partir de principes qui eux-mêmes ne peuvent être démontrés. Il n’y a donc pas de démonstration parfaite au sens où tout serait démontré et tout défini. Ceci n’invalide pas la portée démonstrative des mathématiques mais permet de penser leur idéal comme relatif et non absolu. Pascal part de l’idée d’une mathématique idéale pour montrer les limites de la mathématique réelle et la nécessité de recourir à un autre ordre que le raisonnement pour s’assurer de la vérité de leurs principes.
Enfin la crise contemporaine des fondements en mathématique confirme l’idée selon laquelle leur rigueur formelle repose toujours en dernier sur des énoncés indécidables. Gödel montre que la non-contradiction d’un système formel figure parmi ses indécidables. Il y a une incomplétude des mathématiques du point de vue de leur fondement.
Qu’est-ce qu’un objet mathématique ?
Tout le monde a une idée de ce qu’est un cercle, ou un nombre, mais ces objets ne se rencontrent pas dans le monde réel: ce sont des constructions de l’esprit humain.Parfois, ces constructions sont inspirées par la réalité (on peut facilement se représenter une sphère en observant une bulle de savon), mais la porte reste ouverte à l’imagination.
On appellera ces objets des modèles.
Plus précisément, un modèle sera constitué d’un ensemble (fini ou infini) d’objets, ainsi que de relations entre ces objets, comme par exemple l’ensemble des entiers naturels munis de la relation «plus petit que». De la même manière que les biologistes étudient les organismes vivants, les modèles sont les sujets d’études de la science mathématique. Comment réussir à progresser dans la connaissance de ces modèles?
Puisque ce sont des constructions de l’esprit, on est tenté de faire des déductions purement logiques. Par exemple prenons le modèle des entiers naturels ordonnés :
1, 2, 3 , 4, 5, ……
Si l’on sait que 0 est le plus petit entier naturel, alors on peut en déduire qu’il est plus petit que 5 !
Mais ce type de raisonnement suppose toujours quelque chose de déjà connu.
Quelles déductions pourrait-on faire, si au départ on ne sait rien ?
Il nous faut donc partir d’une base de connaissance : les Axiomes.
Ils sont un ensemble d’énoncés sur notre modèle que nous admettons sans démonstration.
Ce sont souvent des énoncés qui nous semblent évidents dans le modèle que l’on veut étudier.
Cependant, évidents ou non, nous sommes
obligés de les admettre sans preuve pour qu’ils servent de base à des déductions.
Un ensemble d’axiomes s’appelle une théorie.
Par exemple, la géométrie euclidienne que l’on apprend au collège/lycée est une théorie permettant de prouver des théorèmes sur le modèle du plan euclidien contenant des points, droites, cercles, triangles, etc.
L’un des axiomes de cette théorie est:
«Etant donnés 2 points A et B, il existe toujours une unique droite passant par A et B».
On peut voir une théorie comme une description du modèle que l’on veut étudier, au moyen d’axiomes.
On dit qu’une théorie admet un modèle M si tous les axiomes de la théorie sont vrais dans M.
Les théorèmes obtenus par déduction
le seront aussi, si le système de déduction est raisonnable (on ne s’attardera pas sur ce point ici).
Une démonstration(ou preuve) d’un énoncé P est une suite de déductions se basant sur les axiomeset aboutissant à la conclusion que est vrai.
Parfois, on utilisera le mot «théorie» pour désigner non seulement les axiomes, mais aussi tous les théorèmes qui en découlent.En effet, choisir les axiomes fixe instantanément l’ensemble des théorèmes: les conséquences logiques des axiomes ne dépendent pas du fait qu’on trouve une démonstration ou pas!
Imaginez que vous deviez décrire votre chambre dans un petit texte.
Celui qui le lira pourra répondre à certaines questions qu’on lui posera («où est le lit ?», «de quelle couleur est la lampe de bureau ?»).
Le but d’une théorie est le même : décrire un modèle au moyen d’axiomes, de manière à ce que l’on puisse reconstruire ses propriétés par déduction.
Le modèle mathématique correspond donc à la chambre, et la théorie à la description que vous en
faites.
Par exemple si vous dites dans votre description «Tous les objets électriques de ma chambre sont blancs» et «J’ai une radio», on peut démontrer l’énoncé «Il y a une radio blanche», en utilisant les deux axiomes et un raisonnement déductif.
Attention, plusieurs théories sont possibles pour un même modèle (il existe plusieurs manières de décrire la même chambre). C’est au mathématicien de choisir sa théorie, de manière à ce qu’elle décrive le mieux possible le modèle qu’il veut étudier.
Les qualités d’une bonne théorie
Toutes les théories ne se valent pas : elles peuvent décrire plus ou moins bien le modèle, ou même être complètement absurdes.
Elles peuvent aussi être trop compliquées à écrire pour être utilisables en pratique.
Point de vue mathématique
On dit qu’une théorie est complète si elle permet de répondre à n’importe quelle question que l’on peut poser.
Par exemple si votre chambre est vide, ce ne sera pas difficile de la décrire complètement.
Notons qu’on va se restreindre ici aux questions dont la réponse est «oui» ou «non», c’est-à-dire des énoncés qui sont soit vrais, soit faux dans le modèle.
Cela signifie que dans une théorie complète, pour tout énoncé P, on peut toujours trancher sur la véracité de P.
Autrement dit, on peut toujours démontrer soit que P est vraie, soit que P est fausse.
Dans le cas contraire, la théorie est incomplète: vous avez pu oublier de dire s’il y a une fenêtre.
Un lecteur de votre description ne pourra ni affirmer qu’il y a une fenêtre, ni affirmer qu’il n’y en a pas.
Une théorie incomplète est une théorie dans laquelle il existe des énoncés P tels que ni P, ni son contraire ne peuvent être démontrés.
Un tel énoncé P est alors dit indécidable dans la théorie(ou indépendant des axiomes de la théorie).
Dans ce cas, nous sommes sûrs que plusieurs modèles différents peuvent correspondre à notre théorie.
En effet, si la description d’une chambre ne se prononce pas sur la présence d’une fenêtre, alors elle pourrait représenter une chambre sans fenêtre, mais aussi une chambre avec fenêtre
De plus, la théorie est cohérente si ses théorèmes ne se contredisent pas entre eux.
Par exemple, vous ne pouvez pas déclarer que toute votre chambre est blanche, puis affirmer ensuite que le plafond est rouge.
Une théorie incohérente n’a aucune valeur mathématique: si elle permet de démontrer un énoncé et son contraire, alors elle ne peut décrire aucun modèle, car dans un modèle chaque énoncé est soit vrai soit faux.
Pour cette raison, si une théorie admet un modèle, alors elle est forcément cohérente.
La réciproque est également vraie (mais c’est un résultat difficile) : si une théorie est cohérente, alors elle admet un modèle.Bien sûr, l’idéal est d’avoir une théorie à la fois cohérente et complète.
Ainsi, l’on connaitra aussi parfaitement que possible notre modèle, via quelques déductions logiques.
Point de vue pratique
Pour l’instant, nous n’avons imposé aucune restriction sur l’ensemble d’axiomes.
A priori, il pourrait donc être infini, et très compliqué.
Rien ne nous empêche même de déclarer «je prends comme axiome tout ce qui est vrai dans mon modèle».
Ceci nous permettrait d’obtenir facilement une théorie cohérente et complète: dans le modèle chaque énoncé est soit vrai, soit faux.
Cependant, cela ne nous avance pas beaucoup en pratique, car nous ne savons même pas reconnaître les axiomes de notre théorie
On pourrait se restreindre à un nombre fini d’axiomes, mais il se trouve que ceci nous limiterait un peu trop.
On veut parfois avoir une infinité d’axiomes pour définir certaines notions, comme la récurrence sur les nombres entiers par exemple.
Cependant, dans cet exemple, il nous est facile de
reconnaître nos axiomes, car ils sont tous définis selon le même schéma.
Il est donc parfois raisonnable en pratique d’utiliser une infinité d’axiomes.
Où placer la limite entre les théories «raisonnables» et celles qui ne le sont pas?
La réponse est déjà esquissée plus haut: on veut être capable de reconnaître les axiomes de notre théorie.
Formellement, cela veut dire qu’il existe un algorithme (par exemple un programme d’ordinateur), qui nous demande un énoncé, et nous répond «oui» si cet énoncé est un axiome et «non» sinon.
Dans la métaphore de la maison, cela correspond à limiter la description à un nombre fini de mots.
La subtilité étant que ces mots ne décrivent pas directement les axiomes, mais le programme capable de les reconnaître (qui doit, lui, être fini).
Une théorie qui possède un ensemble d’axiomes reconnaissable par algorithme est appelée récursivement énumérable(abrégé RE).
Cette notion possède un intérêt supplémentaire.
Si T est une théorie RE et complète, alors on peut montrer qu’il existe un programme qui reconnaît les théorèmes de T (et non plus seulement les axiomes).
Cela signifie que si l’on veut savoir si un énoncé est un théorème de T, pas la peine de réfléchir à une démonstration, un ordinateur peut faire le travail à notre place.
La théorie est alors dite récursive.
Théorème d’incomplétude
Pendant un temps, l’un des buts affichés des mathématiciens a été de trouver une théorie complète et récursive, qui permettrait de décrire complètement l’ensemble des objets mathématiques
couramment étudiés, et d’avoir en plus un procédé mécanique permettant de tranche sur la véracité de tout énoncé.
En 1931, Kurt Gödel mit fin à de tels espoirs, en publiant son fameux Théorème d’incomplétude.
Dans les grandes lignes, ce théorème affirme que toute théorie RE, cohérente et «suffisamment compliquée» est nécessairement incomplète.
L’exemple de la chambre vide a montré pourquoi il ne faut pas que le modèle décrit soit trop simple.
Plus précisément, « suffisamment compliquée» signifie ici que la théorie doit être capable de parler des nombres entiers, avec les notions d’addition et de multiplication. C’est donc plutôt raisonnable, et les mathématiques de tous les jours sont directement concernées.

La démonstration par le codage de Gödel
L’idée qui se trouve au cœur de la démonstration de Gödel est élégante et novatrice.
Il a remarqué qu’une fois la théorie fixée, tout énoncé mathématique et même toute démonstration peut se coder de façon systématique par un simple nombre entier.
Par exemple on pourra utiliser le nombre 153 pour coder l’énoncé « la somme de deux nombres impairs est toujours paire», et le nombre 19765 pour coder une démonstration de cet énoncé.
Gödel décrit précisément comment passer des énoncés aux codes et vice-versa, mais nous n’entrerons pas dans ces détails ici.
Il parvient ensuite à jouer avec ces codes pour créer un énoncé G qui affirme
«G n’est pas démontrable», en parlant de son propre code.
Si l’on pouvait démontrer G, on tomberait sur une
contradiction, puisqu’il affirme justement que c’est impossible.
Et comme le contraire de G est «G est démontrable», on ne peut pas non plus le montrer!
Du coup la théorie est forcément incomplète : ni G, ni son contraire ne peuvent être démontrés.
Cette astuce rappelle les phrases paradoxales comme « cette phrase est fausse».
Le procédé est cependant un petit peu plus subtil ici: G parle de son code et non directement d’elle-même, comme si vous parliez de votre numéro de sécurité sociale.
Ce codage systématique par des nombres entiers pose les bases de l’informatique.
Aujourd’hui cette idée a fait du chemin : nos textes, nos images, nos musiques, sont enregistrés sur nos disques durs sous forme de code binaire, c’est-à-dire de simples nombres écrits en base 2.
Bien avant l’invention de l’ordinateur, Gödel fut l’un des premiers à imaginer un codage universel, et ce pour montrer un théorème de logique pure !
Par la suite, il a d’ailleurs travaillé activement avec d’autre pères de l’informatique comme Alan Turing,



La numération de Gödel et les métamathématiques
La première étape a consisté à assigner à chaque symbole du système formel un nombre différent.
Puis Gödel a trouvé le moyen d’affecter un nombre à chaque formule (en faisant le produit des premiers nombres premiers élevés à la puissance du nombre représentant les symboles qui y figurent), puis à chaque suite de formule.
L’important est de comprendre qu’un nombre de Gödel étant donné, on peut déterminer si c’est une suite de formules (et si oui de quelles formules elle est composée), une formule (et si oui laquelle) ou un symbole.
Inversement, étant donné un symbole, une formule ou une suite de formules, on peut facilement calculer le nombre de Gödel associé.
Tous ces nombres qui représentent des formules ou des suites de formules représentent donc des faits de l’arithmétique, mais nous pouvons aussi nous intéresser à la méta-arithmétique, qui consiste à parler des faits qui concernent l’arithmétique.
Par exemple, dire que
« Pour tout x, il existe y tel que y > 2x »
est un fait arithmétique, c’est à dire un fait qui concerne les nombres entiers. D’un autre côté, dire que
La formule « Pour tout x, il existe y tel que y > 2x » est démontrable en arithmétique
est un fait meta-arithmétiquen, c’est à dire un fait qui concerne l’arithmétique.
Les formules et suites de formules étant représentés par Gödel sous forme de nombres, celui-ci a ainsi pu exprimer des faits méta-arithmétiques par des formules arithmétiques…
Par exemple, dire qu’une formule de nombre de Gödel g1 contient la formule de nombre de Gödel g2 revient plus ou moins, avec la méthode de Gödel à affirmer que g2 est un diviseur de g1, ce qui une propriété arithmétique, exprimant un fait méta-arithmétique.
Gödel a ainsi réussi à exprimer, en utilisant les nombres de Gödel et l’arithmétique (mais la formule reste assez complexe) que :
La formule de nombre de Gödel g1 est démontrable par la suite de formules de nombre de Gödel g2.
Dans la suite, nous appellerons cette formule G.
La preuve d’incomplétude
La suite du raisonnement a été de montrer que si G était était démontrable, alors la négation de G le serait aussi, et inversement. On aurait alors la possibilité de démontrer une formule et son contraire, ce qui est la définition de l’inconsistance vue plus haut. Par conséquent, si on suppose que le système formel employé est consistant (i.e. que l’arithmétique est consistante), alors on ne peut pas démontrer la formule G ni son contraire. On dit que G est indécidable. Or, la formule G dit que la formule G est indémontrable (rappelons la formule)
n : Il n’existe aucun nombre de Gödel qui représente une suite de formule qui soit la démonstration de la formule portant le nombre de Gödel n
Cette affirmation métamathématique (disant que G est indémontrable) est manifestement vraie, comme nous venons de le voir. Et elle est représentée par une formule arithmétique, selon la méthode de Gödel, qui est donc vraie elle aussi…
Gödel a donc au final construit une formule arithmétique qui est vraie, et qu’on ne peut pas démontrer en utilisant un système formel de l’arithmétique si celui-ci est consistant.
En allant un peu plus loin, Gödel a montré que même en posant comme axiome que G soit vraie, on pourrait toujours trouver une formule vraie et indémontrable, ce qui signifie que si l’arithmétique est consistante, non seulement elle est incomplète, mais le sera toujours même si on y ajoute des axiomes supplémentaires.
Inconsistance de l’arithmétique ?
Par un raisonnement un peu similaire, Gödel a construit une formule, exprimée dans le système formel qui affirme que :
Si l’arithmétique est consistante, alors la formule G est vraie.
Puis il démontre cette affirmation, toujours en utilisant le système formel. Ceci implique que si on pouvait démontrer dans le système formel, que l’arithmétique est consistante, alors, en utilisant la preuve donnée par Gödel, il s’en suivrait que G serait démontrable dans le système formel. Or nous venons de voir que ce n’était pas le cas. Par conséquent, c’est qu’il est impossible de démontrer dans le système formel que l’arithmétique est consistante, ce qui a apporté une réponse au problème de Hilbert…
Discussion sur le Théorème
On pourrait dire que si l’on tombe sur un énoncé indécidable, il suffit de la rajouter en axiome pour compléter la théorie.
Cependant le raisonnement de Gödel s’applique aussi dans cette nouvelle théorie où l’on peut construire, de la même manière, un énoncé indécidable(différent du précédent).
A l’époque, les réactions de la communauté ont été plutôt négatives.
Ce résultat a d’abord été perçu comme une remise en question de la toute-puissance mathématique.
Cependant, certains mathématiciens, à commencer par Gödel lui-même, ont vu dans ce résultat une preuve de «l’inépuisabilité» des mathématiques:
puisque chaque ensemble d’axiomes génère ses propres énoncés indécidables, il existera toujours la possibilité d’enrichir nos théories.
La recherche mathématique serait alors sans fin et n’aurait pour seule limite que celle de l’inventivité des
mathématiciens.
Ce théorème a eu un tel retentissement qu’il a parfois été interprété dans d’autres domaines comme un résultat général d’impossibilité scientifique ou philosophique, voire une limitation intrinsèque
et démontrée de la connaissance humaine
Cependant, gardons bien à l’esprit que, d’une part,ce résultat est un théorème de logique mathématique qui ne doit pas être sorti de son contexte.
Les hypothèses et les conclusions sont très précises et ne s’appliquent tout simplement pas à d’autres systèmes que des systèmes formels.
D’autre part, l’incomplétude démontrée par Gödel est toujours relative à une théorie.
Un énoncé indécidable dans une théorie peut parfaitement l’être dans une autre (qui aura, bien entendu, elle aussi ses propres énoncés indécidables).
En revanche, le théorème de Gödel conduit à se poser des questions philosophiques légitimes sur le statut des modèles que l’on veut étudier.
Peut-on vraiment parler sans ambiguïté des propriétés des nombres entiers, comme si ces nombres existaient dans la nature, alors que nous
n’arrivons pas à les axiomatiser complètement?
Les questions de ce genre sont loin d’être tranchées, et divisent la communauté mathématique en différentes écoles de pensée.
Implications en mathématiques
Ce théorème a mis fin a la quête d’une axiomatisation complète des mathématiques, et de l’arithmétique en particulier. Nous pouvons donc dire adieu à notre programme informatique qui répondrait
à toutes les questions mathématiques.
C’est d’ailleurs une bonne nouvelle pour les mathématiciens, car un tel programme aurait signé la fin de leur profession.
Sur l’arithmétique en particulier, l’espoir d’avoir une théorie RE complète semblait raisonnable, et l’on
disposait de candidats sérieux.
Grâce au théorème de Gödel, on sait maintenant
que certains énoncés résistant aux assauts des chercheurs depuis longtemps ont une chance d’être indécidables.
Un exemple parmi d’autres : la conjecture de
Goldbach affirme que tout nombre pair à partir de 4 est la somme de deux nombres premiers
(un nombre est premier s’il a exactement 2 diviseurs : 1 et lui-même).
Par exemple 6=3+3, 16=11+5, 20=17+3,
etc…
Des milliards de nombres ont été testés par ordinateur, mais la preuve générale attend toujours
d’être trouvée, si jamais elle existe !
Il est à noter que des résultats d’indécidabilité avaient été montrés avant le théorème de Gödel (sur la géométrie d’Euclide par exemple), et d’autres ont été obtenus depuis sans y avoir recours (l’un des plus célèbres concerne les différentes tailles possibles d’ensembles infinis).
Ce théorème peut être vu comme une manière de
générer automatiquement un énoncé indécidable
d’un certain genre, mais ne capture pas tous les énoncés indécidables.
En termes de vérité, on énonce parfois le premier théorème de Gödel sous la forme :
L’ensemble des assertions vraies est strictement plus grand que l’ensemble des assertions démontrables.
En fait, il existe des assertions vraies, pour lesquelles il n’y a pas de démonstration (on ne peut arriver à la solution en un nombre fini d’étapes). Autrement dit, la démonstration des assertions indécidables demanderait une infinité d’étapes. Et sans même aller jusqu’à l’indécidable, on peut imaginer facilement des problèmes dont la complexité dépasse l’échelle humaine. Le premier théorème de Gödel dit qu’il n’y a pas de limite à cette complexité, elle peut croître au-delà de toute borne.
Finalement, comme il a été mentionné plus haut, le théorème de Gödel a été l’un des points de départ
de l’informatique.
En particulier, Kurt Gödel a initié avec (entre autres) Alan Turing et Alonzo Church la théorie de la calculabilité, qui trace les limites entre ce qu’un ordinateur peut faire et ce qui lui est impossible.
Les termes «récursif» et «récursivement énumérable» sont d’ailleurs empruntés à cette théorie, et le théorème de Gödel (considéré avec le recul nécessaire) est l’un des premiers énoncés où ces notions sont utilisées de manière formelle.
Pour aller plus loin :

Gödel a également montré que ni l’ axiome du choix ni l’ hypothèse du continuum ne peuvent être réfutées par la théorie des ensembles acceptée de Zermelo-Fraenkel , en supposant que ses axiomes sont cohérents. Le premier résultat a ouvert la porte aux mathématiciens pour assumer l’axiome de choix dans leurs preuves. Il a également apporté d’importantes contributions à la théorie de la preuve en clarifiant les liens entre la logique classique , la logique intuitionniste et la logique modale .
Ce théorème est l’un des plus importants démontrés au XXe siècle. Voici quelques brèves sélections qui vous aideront à commencer à le comprendre. L’article original de Gödel « On Formally Undecidable Propositions » est disponible dans une traduction modernisée . Il est également imprimé depuis Douvres dans une belle édition bon marché . Voir les théorèmes d’incomplétude de Gödel de Wikipedia pour beaucoup plus.
 Judy Jones et William Wilson, Une éducation incomplète
Judy Jones et William Wilson, Une éducation incomplète
En 1931, le mathématicien d’origine tchèque Kurt Gödel a démontré que dans une branche donnée des mathématiques, il y aurait toujours des propositions qui ne pourraient être prouvées ni vraies ni fausses en utilisant les règles et les axiomes… de cette branche mathématique elle-même. Vous pourrez peut-être prouver toutes les déclarations imaginables sur les nombres dans un système en sortant du système afin de proposer de nouvelles règles et axiomes, mais ce faisant, vous ne ferez que créer un système plus vaste avec ses propres déclarations impossibles à prouver. L’implication est que tout système logique de toute complexité est, par définition, incomplet ; chacun d’eux contient, à un moment donné, plus d’énoncés vrais qu’il ne peut en prouver selon son propre ensemble de règles.
 Le théorème de Gödel a été utilisé pour affirmer qu’un ordinateur ne peut jamais être aussi intelligent qu’un être humain parce que l’étendue de ses connaissances est limitée par un ensemble fixe d’axiomes, alors que les gens peuvent découvrir des vérités inattendues… Il joue un rôle dans les théories linguistiques modernes, qui mettent l’accent sur le pouvoir du langage de proposer de nouvelles façons d’exprimer des idées. Et cela a été interprété comme impliquant que vous ne vous comprendrez jamais entièrement, puisque votre esprit, comme tout autre système fermé, ne peut être sûr de ce qu’il sait de lui-même qu’en s’appuyant sur ce qu’il sait de lui-même.
Le théorème de Gödel a été utilisé pour affirmer qu’un ordinateur ne peut jamais être aussi intelligent qu’un être humain parce que l’étendue de ses connaissances est limitée par un ensemble fixe d’axiomes, alors que les gens peuvent découvrir des vérités inattendues… Il joue un rôle dans les théories linguistiques modernes, qui mettent l’accent sur le pouvoir du langage de proposer de nouvelles façons d’exprimer des idées. Et cela a été interprété comme impliquant que vous ne vous comprendrez jamais entièrement, puisque votre esprit, comme tout autre système fermé, ne peut être sûr de ce qu’il sait de lui-même qu’en s’appuyant sur ce qu’il sait de lui-même.
Carl B. Boyer , Histoire des mathématiques
 Gödel a montré que dans un système rigidement logique tel que Russell et Whitehead avaient développé pour l’arithmétique, des propositions peuvent être formulées qui sont indécidables ou indémontrables dans les axiomes du système. Autrement dit, au sein du système, il existe certaines déclarations claires qui ne peuvent être ni prouvées ni réfutées. Par conséquent, on ne peut pas, en utilisant les méthodes habituelles, être certain que les axiomes de l’arithmétique ne conduiront pas à des contradictions… Cela semble d’avance vouer l’espoir d’une certitude mathématique par l’utilisation des méthodes évidentes. L’idéal de la science, qui consiste à concevoir un ensemble d’axiomes à partir desquels tous les phénomènes du monde extérieur peuvent être déduits, est peut-être également voué à l’échec.
Gödel a montré que dans un système rigidement logique tel que Russell et Whitehead avaient développé pour l’arithmétique, des propositions peuvent être formulées qui sont indécidables ou indémontrables dans les axiomes du système. Autrement dit, au sein du système, il existe certaines déclarations claires qui ne peuvent être ni prouvées ni réfutées. Par conséquent, on ne peut pas, en utilisant les méthodes habituelles, être certain que les axiomes de l’arithmétique ne conduiront pas à des contradictions… Cela semble d’avance vouer l’espoir d’une certitude mathématique par l’utilisation des méthodes évidentes. L’idéal de la science, qui consiste à concevoir un ensemble d’axiomes à partir desquels tous les phénomènes du monde extérieur peuvent être déduits, est peut-être également voué à l’échec.
Ernest Nagel et James R. Newman , La preuve de Gödel
Il a prouvé qu’il était impossible d’établir la cohérence logique interne d’une très grande classe de systèmes déductifs & emdash; arithmétique élémentaire, par exemple &emdash; à moins d’adopter des principes de raisonnement si complexes que leur cohérence interne est aussi sujette à caution que celle des systèmes eux-mêmes… La deuxième conclusion principale est… Gödel a montré que Principia , ou tout autre système au sein duquel l’arithmétique peut être développée, est essentiellement incomplet . En d’autres termes, étant donné n’importe quelensemble cohérent d’axiomes arithmétiques, il y a de vrais énoncés mathématiques qui ne peuvent pas être dérivés de l’ensemble… Même si les axiomes de l’arithmétique sont augmentés par un nombre indéfini d’autres vrais, il y aura toujours d’autres vérités mathématiques qui ne sont pas formellement dérivables de l’ensemble. ensemble augmenté.
Rudy Rucker , L’infini et l’esprit
La preuve du théorème d’incomplétude de Gödel est si simple et si sournoise qu’il est presque embarrassant de la raconter. Sa procédure de base est la suivante :
- Quelqu’un présente à Gödel un UTM, une machine censée être une Universal Truth Machine, capable de répondre correctement à n’importe quelle question.
- Gödel demande le programme et la conception du circuit de l’UTM. Le programme peut être compliqué, mais il ne peut être qu’infiniment long. Appelez le programme P(UTM) pour Program of the Universal Truth Machine.
- Souriant un peu, Gödel écrit la phrase suivante : « La machine construite sur la base du programme P(UTM) ne dira jamais que cette phrase est vraie. » Appelez cette phrase G pour Gödel. Notez que G est équivalent à : « UTM ne dira jamais que G est vrai ».
- Maintenant, Gödel rit de son grand rire et demande à UTM si G est vrai ou non.
- Si UTM dit que G est vrai, alors « UTM ne dira jamais que G est vrai » est faux. Si « UTM ne dira jamais que G est vrai » est faux, alors G est faux (puisque G = « UTM ne dira jamais que G est vrai »). Donc, si UTM dit que G est vrai, alors G est en fait faux et UTM a fait une fausse déclaration. Donc UTM ne dira jamais que G est vrai, puisque UTM ne fait que des déclarations vraies. </li>
- Nous avons établi que l’UTM ne dira jamais que G est vrai. Ainsi, « UTM ne dira jamais que G est vrai » est en fait une affirmation vraie. Donc G est vrai (puisque G = « UTM ne dira jamais que G est vrai »). </li>
- « Je connais une vérité que l’UTM ne pourra jamais dire », déclare Gödel. « Je sais que G est vrai. L’UTM n’est pas vraiment universel.
Pensez-y & emdash; ça pousse sur toi…
Grâce à son grand génie mathématique et logique, Gödel a pu trouver un moyen (pour tout P(UTM) donné) d’écrire une équation polynomiale compliquée qui a une solution si et seulement si G est vrai. Donc G n’est pas du tout une phrase vague ou non mathématique. G est un problème mathématique spécifique dont nous connaissons la réponse, même si UTM ne la connaît pas ! Ainsi, l’UTM n’incarne pas et ne peut pas incarner une meilleure et ultime théorie des mathématiques…
Bien que ce théorème puisse être énoncé et prouvé de manière rigoureusement mathématique, ce qu’il semble dire est que la pensée rationnelle ne peut jamais pénétrer jusqu’à la vérité ultime ultime … Mais, paradoxalement, comprendre la preuve de Gödel, c’est trouver une sorte de libération. Pour de nombreux étudiants en logique, la percée finale vers une compréhension complète du théorème d’incomplétude est pratiquement une expérience de conversion. C’est en partie un sous-produit de la puissante mystique que porte le nom de Gödel. Mais, plus profondément, comprendre la nature essentiellement labyrinthique du château , c’est, en quelque sorte, s’en affranchir.
Douglas R. Hofstadter , Gödel, Escher, Bach : Une éternelle tresse dorée
Toutes les formulations axiomatiques cohérentes de la théorie des nombres incluent des propositions indécidables…
Gödel a montré que la prouvabilité est une notion plus faible que la vérité, quel que soit le système d’axiomes impliqué…
Comment savoir si vous êtes sain d’esprit ? … Une fois que vous commencez à remettre en question votre propre santé mentale, vous êtes pris au piège dans un vortex de plus en plus serré de prophéties auto-réalisatrices, bien que le processus ne soit en aucun cas inévitable. Tout le monde sait que les fous interprètent le monde via leur propre logique particulièrement cohérente ; comment pouvez-vous dire si votre propre logique est « particulière » ou non, étant donné que vous n’avez que votre propre logique pour se juger ? Je ne vois aucune réponse. Cela me rappelle le deuxième théorème de Gödel, qui implique que les seules versions de la théorie formelle des nombres qui affirment leur propre cohérence sont incohérentes.
L’autre analogue métaphorique du théorème de Gödel que je trouve provocateur suggère qu’en fin de compte, nous ne pouvons pas comprendre notre propre esprit/cerveau… Tout comme nous ne pouvons pas voir nos visages de nos propres yeux, n’est-il pas inconcevable de s’attendre à ce que nous ne puissions pas refléter nos structures mentales complètes dans les symboles qui les réalisent ? Tous les théorèmes limitatifs des mathématiques et la théorie du calcul suggèrent qu’une fois que la capacité à représenter sa propre structure a atteint un certain point critique, c’est le baiser de la mort : cela garantit que vous ne pourrez jamais vous représenter totalement.
Pour aller encore plus loin:
Badreddine Belhamissi, Entre le certain et l’incertain, un siècle de controverses sur la fondation des Mathématiques (et de la physique) ou une petite histoire (un peu ) philosophique de l’ordinateur .
RÉFÉRENCES
K. Gödel, Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I.(«Sur les propositions formellement indécidables des Principia Mathematica et des systèmes apparentés ») Monatshefte für Mathematik und Physik, 38 (received 17 novembre 1930, published 1931) Ernest Nagel, James R. Newman, Kurt Gödel, Jean-Yves Girard, «Le théorème de Gödel»Editions du Seuil (1997)
Alan Sokal et Jean Bricmont, «Impostures Intellectuelles». Éditions Odile Jacob, 1997
J.Bouveresse Prodiges et vertiges de l’analogie. De l’abus des belles-lettres dans la pensée, Raisons d’Agir, 1999
Apostolos Doxiadis, Christos H. Papadimitriou, Alecos Papadatos, Annie Di Donna, « Logicomix », Vuibert2010
Blanché et Dubucs, «La logique et son histoire», Armand Colin
Raymond Smullyan, «Les théorèmes d’incomplétude», Dunod
___________
Glossaire:
Système Formel
Un système formel est composé d’une part de conventions qui permettent d’écrire des formules (liste des caractères utilisables et façon de les agencer) et d’autre part de règles de transformation, ou règles d’inférence, qui permettent de transformer une formule en une autre.
Axiome
Dans une théorie, un axiome est une formule de base, que l’on considère vraie sans démonstration. C’est en quelque sorte le « point de départ » qui servira à démontrer des théorèmes.
Théorème
Dans le cadre d’une théorie, un théorème est une formule que l’on peut démontrer comme étant vraie, en partant des axiomes et en procédant par déduction.
Preuve, démonstration
C’est la liste des étapes, non ambiguës (en utilisant les règles d’inférences si on travaille dans un système formel), qui permettent de passer d’une formule supposée vraie à une autre. On obtient alors la preuve que la formule obtenue est vraie.
Méthode axiomatique
Initialement utilisée par Euclide en géométrie, la méthode axiomatique consiste à accepter sans démonstration un petit nombre de vérités (les axiomes) et à les utiliser pour en déduire d’autres choses vraies (théorèmes)
Théorie formelle
Une théorie formelle est composée d’un système formel et d’un ensemble d’axiomes, exprimés dans ce système formel.
Règle d’inférence, règle de transformation
Dans le cadre d’un système formel, les règles d’inférences sont des règles précises, applicables mécaniquement, qui permettent de transformer une formule en une autre, c’est à dire de déduire d’une formule une autre formule.
Consistance
Une théorie formelle est consistante si elle n’admet aucune formule F telle que F et son contraire (non F) puissent être démontrés.
Complétude
Une théorie formelle est complète si il n’existe pas de formule F telle que ni F ni son contraire (non F) ne puissent être démontrés, c’est à dire si tout ce qui est vrai dans la théorie est démontrable dans la théorie.
Machine de Turing
La machine de Turing est le modèle théorique de tous les ordinateurs actuels, et reste particulièrement simple, même si nous ne pouvons pas la détailler ici en quelques lignes.
Programme informatique
Un programme informatique est une suite d’ordres non ambigus qui sont exécutables par une machine de Turing, mais aussi par un être humain, et qui ne laisse aucune part à la réflexion. L’utilisation d’un ordinateur se justifie uniquement par la rapidité d’exécution de ces ordres.