Entre le certain et l’incertain, un siècle de controverses sur la fondation des Mathématiques (et de la physique) ou une petite histoire (un peu ) philosophique de l’ordinateur.
Entre le certain et l’incertain, un siècle de controverses sur la fondation des Mathématiques (et de la physique) ou une petite histoire (un peu ) philosophique de l’ordinateur.
par Badreddine Belhamissi

 Résumé
Résumé
Dans la Calculabilité la théorie des Nombres est le fer de lance du déterminisme et sert de référent [c’est en réalité en dernier ressort l’espace-nodal dans lequel on va immerge les problèmes]et par exemple, la preuve de l’existence de problèmes indécidables dans les systèmes formels (suffisamment complexes pour générer les entiers ) se ramène à la preuve de l’existence d’un problème indécidable en théorie des nombres moyennant la construction d’une isomorphie où les opérations sur les chaînes sont ramenés à des opérations sur les nombres et grâce à un raisonnement diagonal à la manière de Cantor
G.J. CHAITIN: [« Algorithmic information theory ».Cambridge University press. 1987.°]
G.J. CHAITIN a montré que la théorie des Probabilités, fer de lance du non-déterminisme, peut aussi servir de référent aux problèmes de la Calculabilité. Ainsi le célèbre problè me de l’arrêt d’une machine Turing est généralisé en terme de Probabilité d’arrêt d’une machine de Turing.
me de l’arrêt d’une machine Turing est généralisé en terme de Probabilité d’arrêt d’une machine de Turing.
A partir du concept de complexité introduit dans les années 1950 par Kolmogorov, [qui se trouve, par hasard , être aussi le concepteur-stabilisateur de la théorie des Probabilités] Chaïtin développe la notion d’ensembles compressibles et d’ensembles incompressibles qui le conduisent à la notion de programmes minimaux(au sens de Kolmogorov
C’est, ne l’oublions pas, Kolmogorov qui a introduit les K-complexes, en tant que machine abstraite à calculs dès les années 1950 et son concept a été publié pour la première fois en 1954 (en anglais) par son élève et continuateur USPENSKI qui développe son travail en calculabilité .
Machines de Kolmogorov-Uspenski
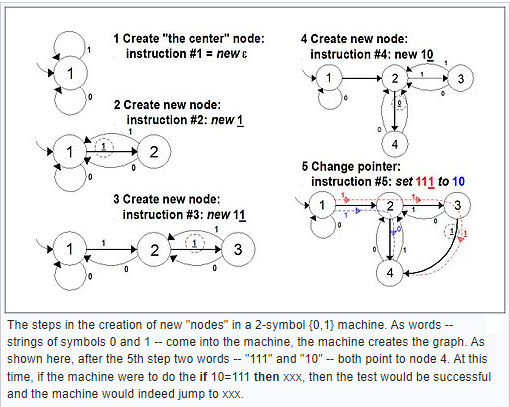 Afin de tester la robustesse de la définition de Turing, Kolmogorov et Uspenski en 1958 imaginent de remplacer le ruban linéaire de Turing par un ruban en forme de graphe non orienté qui peut se modifier au cours du calcul. Lecture, écriture et modification du ruban (suppression ou adjonction d’un nœud) se faisant toujours de façon locale, là où la tête se trouve. On suppose que le graphe reste de degré borné fixé, c’est-à-dire que le nombre de voisins d’un sommet quelconque est toujours ≤ k pour un k fixé indépendant du sommet.Gregory Chaitin défini alors le nombre Oméga comme la probabilité d’arrêt d’une machine de Turing.
Afin de tester la robustesse de la définition de Turing, Kolmogorov et Uspenski en 1958 imaginent de remplacer le ruban linéaire de Turing par un ruban en forme de graphe non orienté qui peut se modifier au cours du calcul. Lecture, écriture et modification du ruban (suppression ou adjonction d’un nœud) se faisant toujours de façon locale, là où la tête se trouve. On suppose que le graphe reste de degré borné fixé, c’est-à-dire que le nombre de voisins d’un sommet quelconque est toujours ≤ k pour un k fixé indépendant du sommet.Gregory Chaitin défini alors le nombre Oméga comme la probabilité d’arrêt d’une machine de Turing.
Chaïtin est probablement le premier chercheur à donner des résultats crédibles sur les renforcements (on pourrait aussi dire les aggravations) du théorème de Gödel, et montre que les choses sont pires que ce que le théorème de Gödel ou le théorème de Turing laissaient prévoir sur les systèmes formels. Oméga, la probabilité d’arrêt d’une machine de Turing s’avère être non seulement être un nombre transcendant mais encore plus difficile que tous les nombres transcendants que nous connaissons comme p ou e qui, eux au moins, ont la bonne idée de se laisser approcher par des algorithmes accélérables. Les limitations des systèmes sont non seulement un question d’actualité réaliste de notre monde technologique mais aussi une caractéristique inhérente des systèmes abstraits.
et montre que les choses sont pires que ce que le théorème de Gödel ou le théorème de Turing laissaient prévoir sur les systèmes formels. Oméga, la probabilité d’arrêt d’une machine de Turing s’avère être non seulement être un nombre transcendant mais encore plus difficile que tous les nombres transcendants que nous connaissons comme p ou e qui, eux au moins, ont la bonne idée de se laisser approcher par des algorithmes accélérables. Les limitations des systèmes sont non seulement un question d’actualité réaliste de notre monde technologique mais aussi une caractéristique inhérente des systèmes abstraits.
En n’hésitant pas à paraphraser Chaïtin nous proposons une lecture détendue et transhistorique de certains événement clés qui nous paraissent être à la source du changement et du devenir du concept que nous avons de la certitude et de la précision dans le monde des mathématiques, en tant que langage déclaré de cette certitude et de cette précision depuis un siècle, mais aussi dans la physique en tant qu’univers ultime de la réalité que décrit ce langage.
 Alan Turing est un mathématicien, cryptologue, pionnier de l’informatique, de l’intelligence artificielle et de la morphogenèse en biologie. Pour résoudre le problème fondamental de la décidabilité en arithmétiques, il présente en 1936 une expérience de pensée que l’on nommera ensuite machine de Turing et des concepts de programme et de programmation, qui prendront tout leur sens avec la diffusion des ordinateurs, dans la seconde moitié du xxe siècle. Son modèle a contribué à établir la thèse de Church, qui définit le concept mathématique intuitif de fonction calculable.
Alan Turing est un mathématicien, cryptologue, pionnier de l’informatique, de l’intelligence artificielle et de la morphogenèse en biologie. Pour résoudre le problème fondamental de la décidabilité en arithmétiques, il présente en 1936 une expérience de pensée que l’on nommera ensuite machine de Turing et des concepts de programme et de programmation, qui prendront tout leur sens avec la diffusion des ordinateurs, dans la seconde moitié du xxe siècle. Son modèle a contribué à établir la thèse de Church, qui définit le concept mathématique intuitif de fonction calculable.
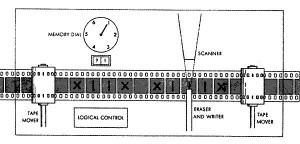
La machine de Turing
Le modèle de Turing est un modèle abstrait d’ordinateur composé d’un mécanisme de calcul et d’un ruban sur lequel la machine écrit et qu’elle peut effacer en déplaçant une tête de lecture-écriture. Chaque machine de Turing est associée à un programme qui détermine avec une précision absolue les opérations qu’elle effectue. Alan Turing démontre qu’il existe un type de machine de Turing (dite universelle) capable de simuler toute autre machine de Turing.
Une fonction Turing calculable est une fonction dont on est capable de construire une description algorithmique de calcul pour une machine de Turing.
Un programme de machine de Turing se compose d’une suite finie composée de symboles. On peut associer à ce programme un nombre appelé index de la machine de Turing.
Les machines de Turing sont énumérables, et donc dénombrables, et on les note Mi.
Le problème de l’arrêt
On démontre qu’il existe des fonctions non calculables : la première d’entre elles est la fonction qui, pour tout programme donné P, indique (a) si le programme finit par s’arrêter ou (b) s’il continue indéfiniment à calculer.
Effectivement, Turing démontre que cette fonction n’est pas calculable, c’est ce qu’on nomme le problème de l’indécidabilité de l’arrêt.
En d’autres termes, il n’existe aucune machine de Turing qui sait déterminer si une autre machine va s’arrêter pour un programme avec une entrée quelconque.
Beaucoup d’autres problèmes sur les machines de Turing ne sont pas décidables.
- Alan Mathison Turing naît le 23 juin 1912 à Londres.
- Son père est administrateur colonial à Madras en Inde.
- Au Malborough Collège, ses dons hors du commun sont vite reconnus.
- Adolescent réfractaire à la culture classique, son goût pour les sciences et son homosexualité le marginalisent à la Sherborne School.
- A 17 ans, Turing comprend les recherches d’Einstein, mais connaît des échecs répétés à ses examens. En 1931, il intègre le King’s College de l’Université de Cambridge où il trouve un milieu plus favorable pour étudier les mathématiques.
AlanTuring âgé de 16 ans | Wikimedia Commons Diplômé en 1933, Alan Turing a lu les publications de Kurt Gödel et de Von Neumann sur le fondement des mathématiques qui influencent ses travaux, grâce auxquels il obtient une bourse d'enseignant chercheur en 1935.
Il résout le problème de la décision défini par David Hilbert, puis s'inscrit en doctorat de logique mathématique à l'Université de Princeton sous la direction d'Alonzo Church, un logicien américain qui est arrivé aux mêmes conclusions. Il développe dans sa thèse la notion d'hypercalcul et appuie sa démonstration sur une "machine universelle", un ordinateur qui est encore une abstraction. Algorithmes, calculabilité - les concepts de la programmation sont posés et la voie est ouverte aux ordinateurs programmables.

En 1939, Alan Turing revient enseigner à Cambridge où il assiste au cours de Wittgenstein qui prétend dissoudre la logique mathématique ! La Seconde Guerre mondiale éclate et Turing s'engage dans l'armée britannique où il travaille à Bletchley Park au déchiffrement des messages de la marine allemande.
Son apport est essentiel, car Turing améliore la "bombe" polonaise, un dispositif qui permet de déchiffrer le code des machines Enigma utilisées par le commandement nazi.


Après la guerre, Alan Turing travaille au National Physical Laboratory et conçoit un prototype de calculateur électronique, l'ACE ( Automatic Computing Engine), qui prend du retard dans sa réalisation. Aussi il rejoint l'Université de Manchester qui avait construit en 1948 le premier ordinateur programmable opérationnel, le Mark 1. Turing participe à la programmation et se passionne pour l'intelligence artificielle. Il élabore un test qui valide l'intelligence d'une machine, le fameux "test de Turing." Parallèlement, il s'intéresse aux phénomènes de croissance animale et végétale qui le conduisent aux « structures de Turing ».
Élu membre de la Royal Society, Turing éprouve de graves difficultés quand la révélation de son homosexualité provoque un scandale en 1952. C'est un crime pour la justice britannique. Le procès le condamne à la prison. Pour éviter l’enfermement, Alan Turing est contraint d'accepter la castration chimique, mais sa carrière est brisée. Il se suicide à 42 ans en croquant une pomme trempée dans du cyanure le 7 juin 1954.
Kolmogorov
 Andreï Nikolaïevitch Kolmogorov (en russe : Андрей Николаевич Колмогоров ) né le 25 avril 1903 à Tambov.
Andreï Nikolaïevitch Kolmogorov (en russe : Андрей Николаевич Колмогоров ) né le 25 avril 1903 à Tambov.
On appelle nombre incompressible au sens de Kolmogorov un nombre réel dont le développement binaire est comparable à la taille de l’algorithme qui permet de le calculer.
En ce sens tous les rationnels et certains irrationnels sont compressibles en particuliers les nombres transcendants comme pi (π ) et e.
A partir du concept de complexité introduit dans les années 1950 par Kolmogorov, [qui se trouve, par être aussi le de la théorie des Probabilités] développe la notion d’ensembles compressibles et d’ensembles incompressibles qui le conduisent à la notion de programmes minimaux(au sens de Kolmogorov, qui n’oublions pas a introduit les K-complexes, en tant que machine équivalente à la machine de Turing, dès les années 1950 et a été publié pour la première fois en 1954 (en anglais), c’est USPENSKI, son continuateur qui développe son travail en calculabilité)
La notion de complexité algorithmique (appelée aussi parfois entropie algorithmique) est apparue dans les années 1960 entre la théorie du calcul, la probabilité
théorie et théorie de l'information.
L'idée d'A. N. Kolmogorov était de mesurer la quantité d'informations
en objets finis (et non en variables aléatoires, comme cela se fait dans le Shannon classique
théorie de l'information). Son célèbre article [78], publié en 1965, explique comment cette
peut être fait (jusqu'à un terme additif borné) en utilisant l'approche algorithmique.
Des idées similaires avaient été suggérées quelques années plus tôt par R. Solomonoff. La motivation de Solomonoff était tout autre. Il a essayé de définir la notion de probabilité a priori.
Imaginez qu'il y ait une expérience (processus aléatoire) et nous ne savons rien de sa structure interne. Pouvons-nous dire quelque chose sur la probabilité de résultats différents dans cette situation ?
On peut mettre cela en relation avec le mesures de complexité indiquant que des objets simples ont une plus grande probabilité a priori
que les plus complexes. (Malheureusement, le travail de Solomonoff n'est devenu populaire qu'après que Kolmogorov l'ait mentionné dans son article.)
En 1965, G. Chaitin (alors étudiant de premier cycle âgé de 18 ans) a soumis deux articles ; ils ont été publiés en 1966 et 1969, respectivement. Dans le deuxième article, il a proposé la même définition de la complexité algorithmique que Kolmogorov.
Les propriétés de base de la complexité de Kolmogorov ont été établies dans les années 1970.
Travaillant de manière indépendante, С. P. Schnorr et L. Levin (qui fut élève de Kolmogorov) ont trouvé un lien entre la complexité et la notion d'aléatoire algorithmique (introduite en 1966 par P. Martin-Löf [115]). Pour y parvenir, ils ont introduit une version légèrement différente de la complexité, la soi-disant complexité monotone. Également
Les idées de Solomonoff sur la probabilité a priori ont été formalisées sous la forme de préfixe de complexité, introduit par Levin et plus tard par Chaitin. Les notions de complexité s'est avéré utile à la fois pour la théorie du calcul et la théorie des probabilités.
La complexité de Kolmogorov est devenue populaire (et pour cause : c'est une base et une notion philosophiquement importante de la théorie des algorithmes) d'après M. Li et P. Vitânyi qui ont publié un livre sur le sujet (première édition parue en 1993).
De Kolmogorov à Chaïtin
Chaïtin à partir de la notion d’ensembles compressibles et d’ensembles incompressibles développe la notion de programmes minimaux (au sens de Kolmogorov.)
Gregory Chaïtin défini le nombre Oméga comme la probabilité d’arrêt d’une machine de Turing.
 |
 « « |
 « « |
| Le nombre Ω appartient à une famille infinie de nombres, les nombres oméga de Chaïtin. Ces nombres oméga sont déconcertants, car chacun concentre une conjonction invraisemblable d’étrangetés. Une sous-classe des nombres oméga de Chaitin, les nombres oméga de Solovay aggravent encore le tableau. Ces classes de nombres bizarres sont aussi importantes que les classes des nombres rationnels, algébriques ou transcendants. |
||
Chaïtin est probablement le premier chercheur à donner des résultats crédibles sur les renforcements (on pourrait aussi dire les aggravations) du théorème de Gödel, et montre avec la découverte des nombres Ω que les choses sont pires que ce que le théorème de Gödel ou le théorème de Turing laissaient prévoir sur les systèmes formels.
Ω est algorithmiquement incompressible donc aléatoire.
Le nombre Ω appartient à une famille infinie de nombres, les nombres oméga de Chaitin. Ces nombres oméga sont déconcertants, car chacun concentre une conjonction invraisemblable d’étrangetés.
Une sous-classe des nombres oméga de Chaitin, les nombres oméga de Solovay aggravent encore le tableau.
Ces classes de nombres Ω bizarres sont aussi importantes que les classes des nombres rationnels, algébriques ou transcendants.
Chaïtin a été surnommé Omega-man par la revue New-Scientist.
|
||||||||||||
|
||||||||||||
Solovay, Robert M.
La probabilité d’arrêt d’une machine de Turing s’avère être non seulement être un nombr e transcendant mais encore plus difficile que tous les nombres transcendants que nous connaissons comme π ou e (la base de la fonction logarithme népérien, notée e, appelée nombre de Néper ou nombre d’Euler.
e transcendant mais encore plus difficile que tous les nombres transcendants que nous connaissons comme π ou e (la base de la fonction logarithme népérien, notée e, appelée nombre de Néper ou nombre d’Euler.
Sa valeur approchée est : e≈2,718281828459045235360….)
qui, eux au moins, ont la bonne idée de se laisser approcher par des algorithmes accélérables.
Un nombre Oméga de Chaïtin est une suite de bits représentant, sous forme concentrée, la solution du problème de l’arrêt pour tous les programmes d’une machine de Turing universelle donnée.
Les limitations des systèmes sont non seulement un question d’actualité réaliste de notre monde technologique mais aussi une caractéristique inhérente des systèmes abstraits.
En n’hésitant pas à paraphraser Chaïtin nous proposons une lecture détendue et transhistorique de certains événement clés qui nous paraissent être à la source du changement et du devenir du concept que nous avons de la certitude et de la précision dans le monde des mathématiques, en tant que langage déclaré de cette certitude et de cette précision depuis un siècle, mais aussi dans la physique en tant qu’univers ultime de la réalité que décrit ce langage.
Métamathématique, vous avez dit ?
Et le langage peut-il se décrire lui-même ?

Alonzo Church,14 juin 1903 Washington 11 aout 1995Alonzo Church est né le 14 juin 1903 à Washington. Il est le fils de Samuel Robbins Church, juge auprès de la cour de district de Columbia, et de Mildred Hannah Letterman Parker. Son arrière grand-père Alonzo S. Church (en) a été professeur de mathématiques et d’astronomie puis président du Franklin College, l’actuelle Université de Géorgie, pendant trente ans. Son grand-père Alonzo Webster Church fut bibliothécaire et bibliographe du Sénat des États-Unis et conseiller général pour le Chicago & Alton Railroad3.
D’après Chaïtin, si on regarde un peu attentivement les écrits des logiciens du début du siècle à la lumière de notre expérience actuelle de l’utilisation intensive de l’ordinateur, on remarque que le lambda calcul d’Alonzo Church est une sorte de langage de programmation fonctionnelle, que le langage de Turing est une sorte de langage machine justement et que les écrits originaux de Gödel contiennent un formalisme qui ressemble furieusement à notre LISP actuel !
Mais, LISP n’est-ce pas ce bon vieux langage qu’a mis au point John McCarthy dans les années 1950 comme exemple de langage à sémantique opérationnelle implémentant les idées sur récursivité des logiciens Italiens dignes élèves de Peano ?
Mais oui c’est bien LISP ce curieux langage qu’on utilise encore aujourd’hui et qui se laisse spécifier par lui-même !
 John McCarthy (né le 4 septembre 1927, à Boston) il est le principal pionnier de l’intelligence artificielle avec Marvin Lee Minsky |
 Marvin Lee Minsky, né le 9 août 1927 à New York et mort le 24 janvier 2016 à Boston, est un scientifique américain. Il a travaillé dans le domaine des sciences cognitives et de l’intelligence artificielle. |
Marvin Lee Minsky est également cofondateur, avec l’informaticien John McCarthy du Groupe d’intelligence artificielle du Massachusetts Institute of Technology (MIT) et auteur de nombreuses publications aussi bien en intelligence artificielle qu’en philosophie comme La Société de l’Esprit (1986)
Le formalisme pour décrire ou pour raisonner ?

David Hilbert est né le 23 janvier 1862 à Königsberg (Prusse orientale).
Il étudie dans le lycée de la ville puis dans son université jusqu’à sa thèse sous la direction de Lindemann, la premier à démontrer que pi est transcendant (ce qui signifie qu’il n’existe aucun polynôme à coefficients rationnels dont pi soit une racine).
Il y enseigne à partir de 1886 jusqu’en 1895, date à laquelle il part à Göttingen.
Il épouse en 1892 Käthe Jeroch avec qui il aura un fils. Il gardera toujours son poste à Göttingen, probablement parce que la ville est alors un centre culturel (pas seulement en mathématiques).
On sait que le projet de Hilbert était de formaliser complètement la Mathématique et le raisonnement Mathématique.
Le 8 août 1900 à Paris, Hilbert énonce un ensemble de 23 problèmes qu’il considère comme fondamentaux et qui effectivement seront des fers de lance de la recherche mathématique du XXème siècle. Il décède le 14 février 1943 à Göttingen.
Hilbert est surtout connu pour les espaces éponymes, qui généralisent la notion de produit scalaire vue en France en première.
Il est également très connu dans le domaine de l’algèbre car il est l’auteur du « théorème des zéros » (en allemand « Nullstellensatz »), un théorème d’une importance capitale, qui pose les bases de la géométrie algébrique.
Il s’est également intéressé à la théorie des nombres et a publié Zahlbericht (Rapport sur les nombres, 1897) où il synthétise notamment les recherches de Kümmer, Kronecker et Dedekind.
En mathématiques, Hilbert est enfin considéré comme le fondateur du courant formaliste.
Ce courant mathématique s’oppose à l’analyse constructive.
Cette dernière n’admet que les preuves constructives (c’est-à-dire les preuves qui lorsqu’elles utilisent un objet en donnent une construction explicite) alors que Hilbert donne plus grande part aux axiomes.
C’est le point de vue de Hilbert qui domine aujourd’hui les mathématiques (même si le point de vue constructif reste étudié par des spécialistes) et c’était même une des idées directrices de la réforme dite des « mathématiques modernes » dans les années 60.
Il a également travaillé en physique, où il est surtout reconnu comme celui qui a apporté les outils nécessaires à Einstein pour formuler la relativité générale (certains lui attribuent même la parenté des équations d’Einstein, mais cette thèse est controversée).
Hilbert fut également un des soutiens de la mathématicienne Emmy Noether.
Très importante pour l’algèbre commutative (certains anneaux portent son nom), elle ne pouvait pas enseigner car les femmes universitaires étaient mal vues en Prusse.
Hilbert l’a autorisée à utiliser son nom pour ses cours.
Une légende raconte qu’Hilbert était tellement distrait qu’un jour où sa femme lui demanda de se changer pour recevoir des invités, il s’est mis au lit après s’être déshabillé.
On dit d’Hilbert qu’il était avec Poincaré (on rapproche souvent ces deux figures) le dernier mathématicien à maîtriser l’ensemble des mathématiques.
Sa devise, gravée sur sa tombe, était « Wir müssen wissen. Wir werden wissen. » (Nous voulons savoir, nous saurons).
Il est amusant de savoir que la veille du jour où il prononça pour la première fois cette phrase publiquement, Gödel déposait sa thèse où il invalide l’objectif de Hilbert.
Gödel et après lui Turing ont montré que cela n’était pas possible.
Mais cet échec de la formalisation du raisonnement a néanmoins été une réussite dans la formalisation des algorithmes, c’est la vraie mèche responsable de l’explosion Babelienne du foisonnement de la technologie actuelle des langages de programmation informatique.
Ce n’est peut-être pas complètement vrai, mais on peut dire que Turing a inventé l’ordinateur pour répondre à la question plutôt philosophique posée par Hilbert.
Il est par ailleurs scandaleusement comique de voir qu’une problématique rationnelle sur la notion de certitude philosophique ait débouché sur une course frénétique et jubilatoire aux supers méga gains dans le marché aux ordinateurs.
Ce que Gödel et Turing ont montré :c’est que le raisonnement axiomatique formel possèdes limitations.
On ne peut formaliser le raisonnement axiomatique dans son entier.
Maintenant, nous devons à la vérité de dire qu’il y a toujours eu des crises dans l’histoire des Mathématiques.
Car la Mathématique, comme les autres domaines du monde abstrait d’ailleurs, évolue et se complexifie.
Les trous de Pythagore
 Une des premières crises fut vécue par les Pythagoriciens quand ils ont dû constater que la racine de deux était irrationnelle.
Une des premières crises fut vécue par les Pythagoriciens quand ils ont dû constater que la racine de deux était irrationnelle.
Cette longueur de la diagonale du carré unité, qui était donc un objet réel, ne pouvait pas s‘écrire comme fraction de deux entiers.
A cette époque le monde des fractions représentait la totalité connue du mode numérique .
Et l’intuition Pythagoricienne qu’à chaque objet réel il corresponde un nombre (et donc une fraction) [et même aussi une signification ]conduisait à concevoir la droite comme une juxtaposition de points représentants ces nombres.
Or donc, la longueur de la diagonale du carré était à la fois dans droite mais en aucun point (i.e. fraction) connu !
On était dans un trou.
L’idée de Pythagore s’écroule, il existe des longueurs incommensurables. Son dogme « tout est nombre » ne retrouvera vie que dans les temps modernes, quand d’autres « objets » seront admis dans le champ des nombres, en particulier, le rapport de la diagonale au côté du carré, racine de 2 que nous disons irrationnel, non pas parce que ce nombre ne serait pas raisonnable mais parce qu’il ne s’agit pas d’un rapport d’entiers.
Se peut-il qu’il existât d’autres nombres que les fractions, des irrationnels, en somme.
La droite de Pythagore était remplie de trous.
(L’histoire montrera que ces trous caractérisent plus fidèlement la droite réelle que les rationnels de Pythagore)
Le fait que c’était une crise justement a survécu actuellement dans le mot même d’irrationnel.
Il faut se souvenir que les Grecs pensaient que la rationalité était l’objectif suprême.
Platon! la Raison !
Si donc un nombre était qualifié d’irrationnel, cela dit tout le trouble vécu à l’époque et on peut considérer que c’était l’équivalent du théorème de Gödel des anciens Grecs.
Il y eut d’autres convulsions mathématiques.
Par exemple, la crise du raisonnement infinitésimal de l’Analyse ou la crise du fameux postulat d’Euclide sur les parallèles et l’émergence des géométries Non-euclidiennes.
Transfinis, Kézako ?
Mais la crise qui nous intéresse est née il y a un peu plus d’un siècle et est dûe au travail de Cantor sur la théorie des ensembles.
 Cantor : Théorie des Ensembles Infinis.
Cantor : Théorie des Ensembles Infinis.
 Déjà Euclide avait démontré que les nombres premiers étaient en nombre infini
Déjà Euclide avait démontré que les nombres premiers étaient en nombre infini
Soit P le nombre premier supposé le plus grand.
// Soit Q le produit plus 1 de tous les nombres premiers inférieur ou égaux à P : Q = 2.3.5.7….P + 1
//Aucun des nombres premiers n’est diviseur de Q; il reste toujours 1.
// Q est soit premier, ou produit de nombres premiers plus grands que P.
// Dans les deux cas, il existe un nombre premier plus grand que P.
// Donc il n’existe pas de nombre premier le plus grand.
// Ils sont en nombre infini.
Même très ancienne, cette démonstration reste aujourd’hui parmi les plus élégantes démonstration mathématiques.
de l’Apeiron à l’Infini
Infini potentiel : infini vu comme un processus qui peut se prolonger arbitrairement longtemps (par exemple diviser une quantité)
c’est Aristote en effet qui distinguait « l’infini actuel » de « l’infini potentiel » dans l’esprit d’Aristote, c’est limite obtenue par divisions successives (convergence)
ou par additions successives (divergence)
Infini actuel : c’est la possibilité de considérer l’infini comme une entité achevée
 Citons Hervé Lehning (Normalien, agrégé de mathématiques) qui nous dit: c’est le véritable infini, celui que refusent les physiciens, c »est l’infini actuel.
Citons Hervé Lehning (Normalien, agrégé de mathématiques) qui nous dit: c’est le véritable infini, celui que refusent les physiciens, c »est l’infini actuel.
Le mot « actuel » doit ici être pris dans le sens de « effectif », comme le « actual » anglais.
L’envisager dans certains calculs est intéressant en mathématiques où la considération de quantités infiniment petites permet de résoudre certains problèmes.
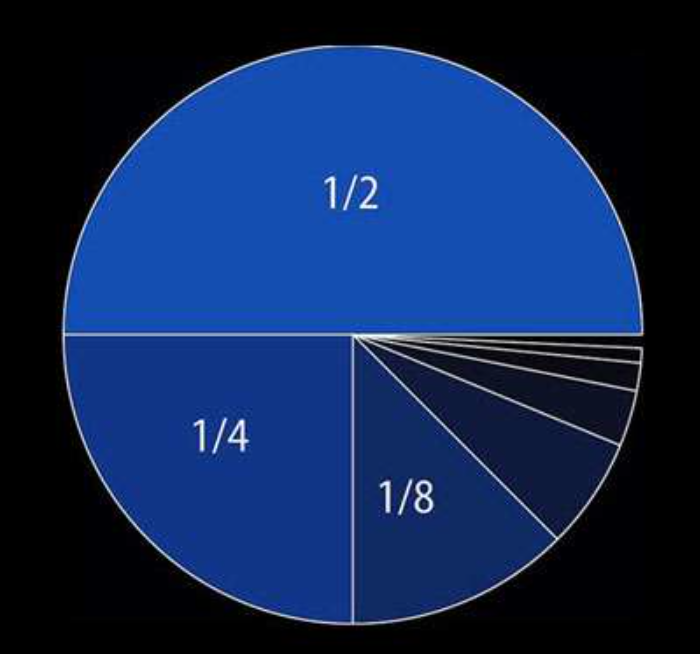
Cette notion permet également de considérer des sommes infinies comme :
S = 1/2 + 1/4 + 1/8 + 1/16 + etc.
Leur donner un sens est une affaire plus délicate.
Dans ce cas, le petit dessin à gauche aide à le faire :
Ce partage géométrique montre que : S = 1.
Il reste que ce partage ne peut se réaliser que dans l’idéal car, très vite, les portions fractionnaires du cercle résultant du processus de la découpe deviennent de plus en plus petites et la limite de notre perception est dépassée.
 L’apeiron (en grec ancien : ἄπειρον / apeiron, « illimité ») est un concept philosophique présenté la première fois par Anaximandre au vie siècle av. J.-C. pour désigner ce principe originel que recherchaient les tenants de l’école milésienne.
L’apeiron (en grec ancien : ἄπειρον / apeiron, « illimité ») est un concept philosophique présenté la première fois par Anaximandre au vie siècle av. J.-C. pour désigner ce principe originel que recherchaient les tenants de l’école milésienne.
Thalès voyait en l’eau le principe originel, la substance de toute chose.
Pour Anaximandre, c’est l’apeiron, qui signifie « illimité, indéfini, indéterminé », qui est le principe et l’élément de tout ce qui existe.
L’apeiron est inaccessible à la sensibilité, mais il doit exister.
Il est nécessaire pour expliquer l’existence de tout ce que nous percevons. Il ne peut posséder de qualité déterminée et n’est désigné que négativement.
 Au 18e siècle, Blaise Pascal écrit, au sujet des deux infinis, l’infiniment petit et l’infiniment grand: » ces extrémités se touchent et se réunissent à force de s’être éloignées, et se retrouvent en Dieu et en Dieu seulement. »
Au 18e siècle, Blaise Pascal écrit, au sujet des deux infinis, l’infiniment petit et l’infiniment grand: » ces extrémités se touchent et se réunissent à force de s’être éloignées, et se retrouvent en Dieu et en Dieu seulement. »
Car enfin qu’est-ce que l’homme dans la nature ?
Un néant à l’égard de l’infini, un tout à l’égard du néant, un milieu entre rien et tout.
Infiniment éloigné de comprendre les extrêmes, la fin des choses et leur principe sont pour lui invinciblement cachés dans un secret impénétrable, également incapable de voir le néant d’où il est tiré, et l’infini où il est englouti.
 Ce symbole était utilisé par les Romains pour représenter 1000, puis un grand nombre.
Ce symbole était utilisé par les Romains pour représenter 1000, puis un grand nombre.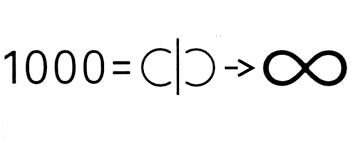
En 1665, John Wallis, Professeur à Oxford, utilisa ce symbole pour désigner l’infini pour la première fois dans » Arithmetica Infinitorum »

« ∞ » ou (U+221E, \infty {\displaystyle \infty }\infty en LaTeX) est le symbole représentant l’infini.
Il a été inventé par le mathématicien John Wallis en 1655 dans De sectionibus conicis (littéralement : des sections coniques), donc antérieurement à Jacques Bernoulli (qui est né en 1654).
Néanmoins, sa forme est similaire à la lemniscate de Bernoulli et à certaines configurations du ruban de Möbius.
Une lemniscate est une courbe plane ayant la forme d’un 8, le terme vient du grec ancien λημνισκος par le latin lemniscus qui signifie justement ruban.
Selon la police d’écriture et la fonte de caractères, ce symbole peut comporter des pleins et des déliés ou non, modifiant ainsi sa symétrie.
 Symbole utilisé par Euler pour désigner l’infini.
Symbole utilisé par Euler pour désigner l’infini.
Une variante non fermée du symbole, plus du tout usitée dans la typographie, a été couramment utilisée au xviiie siècle,
en particulier par Leonhard Euler, qui l’appelle absolutus infinitus, par opposition à 
d’autres quantités infinies qu’il construit à partir de ce « nombre infini absolu »
(comme son logarithme par exemple).
Le symbole de proportionnalité ∝ est également assez similaire.
Usage dans les notices biographiques
On emploie parfois le signe de l’infini dans les notices biographiques comme symbole du mariage.
Accolé à une date, il indique celle de la cérémonie.
Mais, il ne fut généralisé qu’en 1713 grâce à son adoption par Bernoulli.
Jacques ou Jakob Bernoulli (1654-1705) est un mathématicien et physicien suisse (né et mort à Bâle)

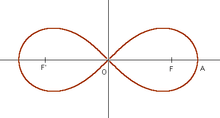

Le symbole actuel de l’infini qui n’est autre la lemniscate de Bernoulli stylisée (il représente un huit couché ou huit paresseux.
en mathématique, c’est une lemniscate dont on peut suivre le parcours indéfiniment (à rapprocher aussi du ruban de Möbius et de son parcours pareillement indéfini).) était déjà utilisé par les romains pour représenter 1000, puis un grand nombre.
 Au 19e siècle, Bolzano publie Les paradoxes de l’infini. Avec lui commence l’histoire moderne de l’infini mathématique. Il découvre que le cardinal des segments [0,1] et celui du segment [0,2] sont identiques.
Au 19e siècle, Bolzano publie Les paradoxes de l’infini. Avec lui commence l’histoire moderne de l’infini mathématique. Il découvre que le cardinal des segments [0,1] et celui du segment [0,2] sont identiques.
Il est le premier à défendre l’idée que l’infini peut être introduit en calcul mathématique et dans le calcul infinitésimal en particulier.
Il est le premier à fonder une vision mathématique de l’infini actuel.
En caractérisant un ensemble par ses propriétés, sa totalité est appréhendée. Inutile d’énumérer tous les éléments.

Bernard Bolzano (1781-1848) est le premier à défendre l’idée que l’infini peut être introduit en calcul mathématique et dans le calcul infinitésimal en particulier.
Questions sur les ensembles infinis
L’introduction des ensembles infinis pose des problèmes nouveaux et délicats.
Y a-t-il plusieurs sortes d’ensembles infinis ?
Sont-ils tous de la même taille ?
Peut-on les comparer entre eux ?
Est-ce que tout ceci a un sens ? Est-ce que ¸ca a un sens de parler de la « taille » d’un ensemble infini, et si oui, avec quelle unité la mesurer ?
Les ensembles infinis aboutissent parfois `a des situations qui défient un peu l’intuition.
Question 1 : y a-t-il autant d’entiers naturels que d’entiers naturels pairs ?
Les nombres pairs sont bien sûr : 0, 2, 4, 6, 8, 10, … , 98, 100, … , 998, 1000, etc.
Il y en a bien sûr une infinité…
Construisons ce qu’on appelle une correspondance biunivoque entre chaque entier et chaque nombre pair
à tout entier naturel n, on associe l’entier naturel 2n, qui est pair.
on obtient le tableau suivant:

On peut constater que chaque entier naturel n correspond au nombre pair 2n, et réciproquement on peut « relier » tout nombre pair 2n à l’entier naturel n et ceci peut se faire indéfiniment
n est obligé de constaté qu’il y a donc autant d’entiers naturels que d’entiers naturels pairs !
Alors qu’intuitivement, il y a « deux fois plus d’entiers naturels » que d’entiers naturels pairs.
Question 2 : y a-t-il autant d’entiers naturels que d’entiers relatifs ?
On aurait tendance à dire non puisque les entiers relatifs sont composés des entiers naturels auxquels on ajoute les entiers négatifs
et pourtant on peut construire facilement une correspondance biunivoque entre l’ensemble des entiers et l’ensemble des entiers relatifs:

Autrement dit, à tout entier naturel n, on associe l’entier 2n, et à tout entier strictement négatif n on associe l’entier impair -2n-1. Et réciproquement…
Donc, on en déduit contrairement à notre intuition qu’il y a autant d’entiers que d’entiers relatifs.
De même, on pourrait montrer que que le nombre infini des entiers N est égal à l’infini de l’ensemble des carrés, des cubes, etc.
Il semble bien donc qu’il existe un unique infini, qu’on peut appeller infini dénombrable, puisque tous les autres ensembles infinis peuvent se ramener à celui des entiers naturels (dénombrable).
Question 3 : y a-t-il autant d’entiers naturels que de nombres réels ?
La réponse est NON, et ce fut découvert en 1891 par Georg Cantor : c’est l’argument de la diagonale de Cantor.
Supposons qu’on puisse numéroter une liste (quelconque) de réels de l’intervalle [0 ;1] :
r1 = 0, 0 1 0 5 1 1 0 …
r2 = 0, 4 1 3 2 0 4 3 …
r3 = 0, 8 2 4 5 0 2 6 …
r4 = 0, 2 3 3 0 1 2 6 …
r5 = 0, 4 1 0 7 2 4 6 …
r6 = 0, 9 9 3 7 8 1 8 …
r7 = 0, 0 1 0 5 1 3 0 … etc.
Le nombre obtenu à partir de la diagonale est : 0,0140210…
En changeant chaque décimale par sa suivante, on construit alors le nombre : 0,1251321…
Ce nombre ne peut être dans la liste ci-dessus, car il diffère de r1 par sa première décimale, de r2 par sa deuxième décimale, de r3 par sa troisième décimale, etc.
Autrement dit, pour toute liste dénombrable de réels de [0 ;1], on peut construire un réel de [0 ;1] qui n’est pas dans cette liste.
Conclusion : l’ensemble infini des nombres réels est strictement plus grand que l’ensemble infini des entiers N
De même Cantor a répondu oui à la Question 4 : y a-t-il un infini plus grand que celui des réels ?
En fait depuis l’analyse du mouvement par Galilée et surtout avec le calcul infinitésimal inventé à la fois par Newton et Leibniz.
Un nouveau tournant survient avec et de nouveaux concepts mathématiques apparaissent : celui de fonction, de dérivée, de suite et de série infinie, de limite, de quantité infinitésimale, de différentielle, etc ».
L’idée est de calculer la longueur d’une courbe en faisant la somme d’une infinité de portions de droites qui s’approchent le plus d’elle.
Cette méthode puissante démontrera que la notion d’infini peut être utilisée dans les mesures mathématiques.
 C’est Georg Cantor (1845-1918), qui découvrira de nombreuses propriétés des tailles d’ensembles infinis qui lui sembleront souvent à la limite du paradoxe.
C’est Georg Cantor (1845-1918), qui découvrira de nombreuses propriétés des tailles d’ensembles infinis qui lui sembleront souvent à la limite du paradoxe.
Cantor distinguera les tailles des ensembles.
Si le contraire avait été vrai (c’est-à-dire si chaque ensemble infini avait pu être mis en bijection avec chaque autre), la théorie de la taille des ensembles infinis aurait singulièrement manqué d’intérêt !
Cantor s’aperçoit, en 1874, que l’ensemble des nombres réels ne peut pas être mis en bijection avec l’ensemble des nombres entiers : il est de taille strictement plus grande.</table
Le raisonnement diagonal que Cantor découvre en simplifiant son raisonnement de 1874 sera le prototype même du raisonnement permettant de démontrer des résultats d’impossibilité en mathématiques.
Dans ce théorème, on suppose que ce qu’on veut établir est faux (ici, qu’il existe une bijection entre l’ensemble ℕ des entiers et l’ensemble ℝ des réels), puis on joue sur la diagonale du tableau qu’elle définit (le i-ème chiffre du nombre réel f(i)), et l’on déduit une contradiction.>
Mieux (ou pire !), Cantor montre, toujours par un raisonnement diagonal, qu’il existe une infinité de tailles possibles différentes pour les ensembles infinis.
Plus précisément, un ensemble E ne peut jamais être mis en bijection avec l’ensemble de ses parties, noté P(E).
L’ensemble P(ℕ) des parties de ℕ (qui est composé de l’ensemble des nombres pairs, de l’ensemble des nombres premiers, etc.) ne peut pas être mis en bijection avec ℕ.
De même, l’ensemble P(P(ℕ)) (ensemble des parties de l’ensemble P(ℕ)) ne peut pas être mis en bijection avec P(ℕ) ; etc.
Ces résultats constituent une première avancée dans la compréhension de l’infini actuel et la preuve que ce qu’on découvre est digne d’intérêt : les résultats construisent une hiérarchie des totalités infinies où l’esprit trouve ses repères. Ces premiers résultats ne sont pas sans soulever réprobations et critiques. Le célèbre mathématicien Kronecker est particulièrement sévère et il bloquera un manuscrit de Cantor en en retardant la parution dans le Journal de Crelle, l’un des plus prestigieux journaux de mathématique, auquel Cantor refusera par la suite de proposer ses travaux.
d’après Jean-Paul Delahaye Mathématicien Informaticien Publié le 03/02/2013 Modifié le 24/04/2017 dans le site Futura Sciences.Georg Cantor Formellement la notion d’infini s’impose en 1873 grâce aux travaux de Georg Cantor
Formellement la notion d’infini s’impose en 1873 grâce aux travaux de Georg Cantor
Georg Cantor naît en 1845 à Saint-Petersbourg, d’une mère russe et d’un père homme d’affaires allemand, d’origine juive mais converti au protestantisme. Il passe ses premières années en Russie. La famille revient en Allemagne quand Georg a onze ans, d’abord à Wiesbaden puis à Francfort.
Le cardinal d’un ensemble est généralisé à la notion de puissance d’un ensemble dans le cas infini
Dans Les paradoxes de l’infini, Bolzano (1781-1848) allait d’abord affranchir la notion de l’infini actuel de celle de Dieu en la situant dans le champ du calcul et de la quantification plutôt que dans celui de la théologie.
Pour cela, il partit de l’idée simple que quand on compare deux ensembles finis, pour qu’ils aient le même nombre d’éléments, on dit le même cardinal, cardinal étant le nombre d’éléments d’un ensemble, il suffit de pouvoir associer à chaque élément d’un ensemble un élément et un seul de l’autre et réciproquement..
Il généralisa cette idée aux ensembles infinis : deux ensembles infinis sont égaux, en terme de nombre d’éléments, s’il est possible d’établir une correspondance biunivoque entre les éléments de ces deux ensembles, c’est-à-dire s’il est possible d’associer un élément du second ensemble à chaque élément du premier et réciproquement…
Bolzano a ainsi utilisé une démarche typiquement mathématique : définir rigoureusement un concept aussi général et abstrait que possible, ici l’infini actuel, de façon à ce que l’utilisation de cette définition permette des raisonnements cohérents..
Il ne s’agit donc pas de se demander ce que peut représenter cet infini actuel dans notre monde et l’évaluer selon un critère de vérité.Cette définition a eu des conséquences contraires à l’intuition. En effet comparons l’ensemble des nombres entiers positifs, N, et celui des nombres pairs..
À chaque nombre entier on peut associer un nombre pair et un seul, son double. .
Réciproquement, à chaque nombre pair on peut associer un nombre entier et un seul, sa moitié..
Il existe donc une relation biunivoque entre les entiers et les nombres pairs, deux ensembles infinis. .
Selon la définition de Bolzano, ces deux ensembles ont le même nombre cardinal, ils ont la même infinité d’éléments. .
C’est peu intuitif car les nombres pairs sont inclus dans les entiers qui en plus incluent les nombres impairs ! .
En fait, la définition de l’infini implique qu’un ensemble infini peut avoir le même cardinal qu’une de ses parties, infinie elle aussi ! .
Ce résultat allait contre ce qui semblait être une évidence depuis Aristote..
Les nombres constituèrent la porte d’entrée principale pour l’étude de l’infini. .
En calcul, la suite des nombre entiers est probablement le premier contact que l’on a avec l’infini.
Cantor, d’emblée, affirma l’existence de l’infini actuel. Il osa ce que personne n’avait osé depuis Aristote :la suite des entiers positifs (0, 1, 2, 3, … ) est infinie, l’ensemble des entiers positifs, N, est donc un ensemble qui a une infinité d’éléments, alors il affirma que le cardinal de cet ensemble était un nombre qui existait comme tel sans que l’on utilise le symbole fourre-tout ∞,il l’appela ℵ0.Le symbole ℵ est la première lettre de l’alphabet hébreu et se prononce aleph, ℵ0 se prononce aleph 0.Il faut signaler que Cantor est resté un juif très croyant, ce qui le tourmentera durant toute sa réflexion sur l’infini.
Cantor allait nommer ce nombre étrange, un nombre transfini, il représentait une quantité infinie.
L’acte décisif fut d’affirmer qu’il y a, après le fini, un transfini, c’est-à-dire une échelle illimitée de modes déterminés qui par nature sont infinis, et qui cependant peuvent être précisés, tout comme le fini, par des nombres déterminés, bien définis et distinguables les uns des autres. (La Recherche, # 268, p. 908).
En 1883, Cantor écrivit :Ne pas simplement considérer l’infiniment grand sous la forme de ce qui croit sans limite, mais également le fixer de façon mathématique par des nombres, cette pensée s’est imposée à moi logiquement, presque contre ma volonté.
Cantor montre que le nombre de points sur une droite est plus infini (transfini, disait-il) que l’infini des nombres entiers.
C’est la puissance du continu, dit-il.
HenriPoincaré

n’adhérait pas à ce concept
La lettre cabalistique en hébreu est aleph (Ж ) qui sera utilisée par Cantor pour nommer les différents infinis mathématiques
L’infini implique plutôt un processus illimité que quelque chose » en acte « , pouvant être identifié. Certains pensent que l’infini n’existe pas en tant que quantité, mais seulement que comme un potentiel:
une quantité qui peut toujours devenir plus grande ou plus petite sans que jamais ce devenir ne se transforme en être.
L’infini a-t-il une réalité, ou bien est-il une fiction utile au calcul comme le pensait Leibnitz?
Cantor donna une autre idée de l’infini:
le seul ensemble infini » en acte « , pouvant être équivalent à des parties de lui-même.
Par exemple, l’ensemble infini des nombres pairs est équivalent à l’ensemble infini des nombres entiers dans sa totalité.
En 1873 Cantor prouve que l’ensemble des nombres rationnels est dénombrable (pouvant se mettre en correspondance biunivoque avec l’ensemble des Entiers), un an avant il avait montré suite aux travaux de son ami Dedekind que l’on pouvait définir les nombres irrationnels comme limites de séries convergentes de rationnels.
Il montre aussi, que l’ ensemble des nombres algébriques, c’est à dire l’ensembles des nombres solutions des équations polynomiales à coefficients rationnels, est dénombrable.
La démonstration de Cantor n’est pas difficile.

(texte d’après Nicolas Oresme, Université de Caen)
En décembre 1873 il montre que l’ensemble des nombres réels n’est pas dénombrable.
Un nombre transcendant est un nombre qui ne peut pas être solution d’une équation polynomiale à coefficient rationnels.
1851-Liouville En 1851 Liouville avait établi l’existence de tels nombres.
Cantor venait donc de démontrer que presque tous les nombres réels étaient des nombres transcendants !
En 1874, à la question de Dedekind
sur l’existence ou non, et Dedekind pensait que non, d’une correspondance biunivoque entre l’intervalle des nombres réels [0,1] et les points du carré unitaire fermé ([0,1]x[0,1]),
Cantor démontre l’existence d’une correspondance biunivoque entre les nombres réels de l’intervalle [0,1] et l’ensemble des points d’un espace à p dimensions.
Il écrit à son ami : « Je le vois, mais je n’y crois pas ! »
Il existe donc un certain nombre d’ensembles infinis équivalents.
R est en bijection avec tout intervalle de longueur non nulle
R est en bijection avec P(N) [ensemble de tous les sous-ensembles de N]
R est en bijection avec R 2 Cantor a longtemps cherché et cru que c´était faux mais il découvre à sa stupéfaction que R est en bijection avec R 2 .

Julius-Wilhelm-Richard-DedekindVoici sa preuve de façon résumée :
R ←→ P(N) ←→ P(Z) ←→ P(Z ∗ −) × P(Z+)
R ←→ P(N) 2 ←→ R 2
– R est en bijection avec R n ; – cela implique en particulier que R est en bijection avec tout R-espace vectoriel et tout C-espace vectoriel .
Démonstration de l’existence d’une bijection entre R et RnsourceDans une lettre, adressée le 20 juin 1877 à Dedekind , Cantor donne la première démonstration de l’existence d’une bijection entre R et Rn (où R désigne l’ensemble des nombres réels).Plus précisément il montre l’existence d’une bijection entre le segment [0 , 1] (l’ensemble des réels compris entre 0 et 1) et le carré [0 , 1]2 (l’ensemble des couples de réels (x, y), tels que x et y soient compris entre 0 et 1).L’argument est le suivant :Si x est un réel compris entre 0 et 1, on peut considérer l’écriture «décimale illimitée», selon l’expression de Cantor, de tout réel qui s’écrit d’une façon et d’une seule sous la formex = 0, α1 α2 α3 … αn …. où αn est la nème décimale du nombre réel x.Pour construire une bijection de [0 , 1]2 dans [0 , 1] il faut associer à un couple de réels (x, y) (compris entre 0 et 1) un réel z (toujours compris entre 0 et 1) ; l’idée de Cantor est de procéder comme suit :Si x = 0, α1 α2 α3 … αn …. et y = 0, β1 β 2 β 3 … βn ….On pose z = 0, α1 β1α2 β 2 α3 β 3… αn βn ….La (2n – 1)ème décimale de z est donc la nème décimale de x et la (2n)ème décimale de z est la nème décimale de y.Il est facile de vérifier que cette application est bijective.Dans sa lettre, Cantor donne une solution un peu plus générale que celle-ci, montrant directement l’existence d’une bijection entre [0 , 1] et [0 , 1]n pour tout entier n, mais le principe de la démonstration est celui décrit ci-dessus.
Enfin le fait d’avoir montré l’existence d’une bijection entre [0 , 1] et [0 , 1]n permet de déduire celle d’une bijection entre R et Rn.
Il existe en effet des bijections entre un segment des réels et l’ensemble de tous les réels (par exemple l’application tangente) et il est ensuite facile de vérifier que deux segments quelconques (non vides) sont en bijection entre eux.
La surprise de Cantor devant ce résultat vient d’une certaine confusion, qui sera précisément levée par ses travaux, entre dimension d’espace vectoriel et cardinal d’un ensemble.
En tant qu’espaces vectoriels, R et Rn sont très différents. Mais en tant qu’ensemble de points, ils sont en bijection et ont donc le même cardinal.
Le premier résultat fondamental de la théorie des cardinaux, a consisté à montrer qu’il n’existe pas de bijection entre l’ensemble des entiers et celui des réels (lettres de novembre-décembre 1873 à Dedekind), ouvrant la voie à l’idée de hiérarchie des infinis.
Celle-ci sera établie de façon générale par le « théorème de Cantor », énonçant qu’il n’existe pas de bijection d’un ensemble dans son ensemble des parties.
L’existence d’une bijection entre R et Rn une sorte de pendant positif du théorème de Cantor, montrant que des ensembles infinis, très différents d’un point de vue mathématique, ont néanmoins même « nombre d’éléments ».
Ce sont ces deux résultats qui montrent la richesse de la théorie cantorienne des cardinaux.
Mais alors, pourquoi pas une infinité?
Une infinité d’ensembles infinis!
C’est un infini d’ordre 2.
Alors pourquoi pas l’ordre 3, puis 4, ou … même, infini.
Ces ensembles d’ensembles infinis sont bien sûr en nombre infini.
On peut encore continuer comme ça…jusqu’à l’infini!
Ce serait alors, l’infini absolu, le vrai.
Le plus grand infini concevable.
Il est noté » ωp
Donc Cantor était obsédé par la notion d’infini et peut-être pas seulement pour des raisons théologiques.
Cantor a eu l’idée d’ajouter à la suite infinie des Entiers, 1, 2, 3,. . .la dernière lettre de l’alphabet Grec oméga, ω qui devenait le premier nombre après tous les nombres finis : c’était le premier nombre transfini.
On peut alors écrire
1,2,3,…, ω+1, ω+2, ω+3,….
Puis, on se dit pourquoi s’arrêter là, en effet on peut continuer 1,2,3,…, ω, ω+1, ω+2, ω+3,…
jusqu’à 2ω, 2ω+1, 2ω+2, 2ω+3,…
puis après 3ω,…,4ω,…
jusqu’à donc ω2 .
1,2,3,…, ω+1, ω+2, ω+3,….2ω 3ω 4ω … ω2
1,2,3,…, ω+1, ω+2, ω+3,…. 2ω 3ω 4ω … ω 2 …ω3… ω4… ωω… ωωω
C’est enivrant ; après un moment on ne sait plus réellement ni où on est ni où on va.
Le nombre suivant est w élevé à la puissance w de façon indéfinie, ce qui donnerait
ωωωωωωωωωωωωωωωωωωωωω…
Ce nombre est la plus petite solution de l’équation
x = ωx
Ce nombre est dénommé, on ne sait pas trop pourquoi, ε0 (Epsilon zéro).
Comme on le voit cette approche est d’une puissance imaginative fantastique et on ne sait plus si c’est vraiment encore tout à fait des mathématiques.
Comme on le voit cette approche est d’une puissance imaginative fantastique et on ne sait plus si c’est vraiment encore tout à fait des mathématiques.

Leopold-Kronecker
Poincaré, le grand mathématicien Français parle lui de désastre à propos de cette théorie , Kronecker lui traite carrément Cantor de corrupteur de la jeunesse !
Mais la topologie moderne et un grand nombre parmi les résultats de mathématique les plus abstraits du 20 ème siècle en découlent directement en tant que généralisations.
En fait on peut dire que la mathématique du 19 ème siècle était moins abstraite et plus concernée par les cas spéciaux et les formules comme les séries infinies de Taylor par exemple.
La mathématique du 20 ème siècle est arrivée au niveau d’abstraction des ensembles théoriques.
Cela est dû pour une part à Cantor qui est accusé d’avoir fait perdre sa partie concrète aux mathématiques en passant par exemple de l’analyse pure et dure à l’analyse théorique !
En fait ceci est très controversé.
Et, ce qui n’aide pas beaucoup, non seulement nous sommes en pleine controverse mais en fait nous avons aussi des contradictions.
Et c’est là plus qu’une simple opinion.
Il existe certains cas où on ne peut pas ne pas être gravement troublé par le non-sens obtenu.
Ainsi il existe un théorème de Cantor qui dit que pour tout ensemble infini, il existe un ensemble infini plus grand qui est l’ensemble de tous les sous-ensembles de cet ensemble , ce qui semble résonner de façon très raisonnable.
C’est le fameux argument diagonal de Cantor.
Argument diagonal de Cantor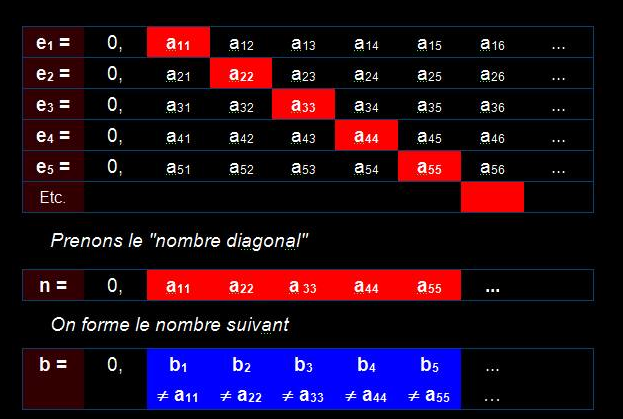
Comment faire la liste de tous les nombres imaginables, et, cependant, en trouver encore d’autres ? Comment prouver qu’il existe plus d’un seul type d’infinis !
Nous allons prendre les nombres décimaux compris entre 0 et 1;
ceux qui commencent par 0, …
Avec la règle de la diagonale de Cantor,
il est toujours possible de former un nouveau nombre, quel que soit l’inventaire que nous puissions produire.
b est bien un réel compris entre 0 et 1 et, par construction, il n’appartient pas au tableau de correspondance.
C’est un nombre en plus!
L’application de la diagonale de Cantor montre que le tableau ne contiendra jamais tous les nombres réels.
Soit N l’ensemble des entiers naturels qui est infini et dénombrable.
Alors Cantor a prouvé un théorème qui dit que
Théorème L’ensemble 2 N est non-dénombrable. (où 2N est l’ensemble de tous les sous-ensembles de N)
Preuve :Supposons que 2 N est infini et dénombrable alors on peut le mettre en bijection avec N.
On peut alors mettre en correspondance les éléments de N et les élément de 2 N c’est à dire qu’on peut NUMÉROTER les éléments de 2 N, la numérotation serait biunivoque et formellement alors :
il existerait une application bijective
f : N ————> 2 N
et donc on pourrait numéroter 2 N
de la façon suivante 2 N= {S0 , S1 , S2 ,. . . }
où Si =f(i) pour tout i ∈ N.
Considérons alors l’ensemble suivant
D={n∈N : n∉ Sn }
autrement dit D est un ensemble d’entiers naturels
ce pourrait être donc un certain sous-ensemble S k pour un certain nombre naturel k.
posons donc D= S k
Maintenant posons-nous la question de savoir si k peut être dans S k c’est à dire si k ∈ S
(1) supposons que oui
k ∈ S k de par la définition de D
il s’en suit que k ne peut appartenir à D={n∈N :n∉Sn }
mais D= S k et donc k ∉ S k est une contradiction.
(2) Maintenant supposons que k ∉ S k;
alors k appartient à D mais D lui-même n’est autre que S k
Donc k est dans S k est une autre contradiction.
Comme ni(1) ni(2) ne peut être possible l’hypothèse que D= S k pour un certain k doit être une erreur .
Donc 2 N est non dénombrable
Récapitulons pour voir comment fonctionne le principe de la diagonalisation.
L’ensemble D est en fait un ensemble diagonal pour la relation : R={(i,j) : j∈f(i) }
comme Si =f(i) , l’ensemble R i ={j :(i,j) ∈R} est tout simplement Si.
Maintenant on s’attend à ce que D diffère de tous les ensembles R i
c’est à dire de tous les Si et c’est ceci justement qui sera prouvé par contradiction. Comme D est différent de chaque Si , D∉ f(N) et donc l’hypothèse que f était une bijection est hypothèse incorrecte
On a donc prouvé qu’il existe un sous-ensemble de N qu’il n’est pas possible de numéroter.
Que donc N et 2 N ne peuvent pas être isomorphes
et malgré que N soit infini on a prouvé que 2 N contient strictement plus d’éléments et est en quelque sorte plus grand .
Paradoxalement votre
Donc si on est convaincu de cela, que se passe-t-il si on applique le théorème à l’ensemble Universel ?
L’ensemble Universel est l’ensemble toute chose; c’est l’ensemble dont la fonction caractéristique des éléments est 1 pour tout objet .
Tout objet appartient à cet ensemble.
En considérant l’ensemble de tous les sous-ensembles de cet ensemble Bertrand Russell a détecté un fameux problème.
- les redoutables paradoxes de Bertrand Russel viennent tout ébranler, alors qu’ils paraissent pourtant enfantins : Peut-on par exemple parler de l’ « ensemble de tous les ensembles » ?
- Si c’est un ensemble, il doit se contenir lui-même?
- Sinon, ce n’est pas un ensemble ?
- Pire, le fameux « paradoxe du barbier » : imaginez un pays dans lequel il n’y a qu’un barbier, et que celui-ci rase tous les gens qui ne se rasent pas eux-mêmes, et seulement ceux-ci.
- Nous nous retrouvons avec deux ensembles bien définis. Mais qui rase donc le barbier ?
- S’il se rase lui-même, le barbier ne devrait pas le raser, mais c’est lui le barbier !
- Et s’il ne se rase pas, alors le barbier (lui, donc) devrait le raser.
- Vous suivez ?! On ne s’en sort pas, c’est un cauchemar.
- Bref, les meilleurs mathématiciens et logiciens suaient sang et eau sur ce problème au début du XXe siècle (le même Russel, dans un travail commun avec Whitehead, vont jusqu’à prendre 350 pages pour démontrer… que 1 + 1 = 2 !)
- Pendant ce temps, d’autres mathématiciens, et non des moindres, trouvaient ce travail inutile : pour eux, cette démarche enlève tout son sens aux mathématiques, celles-ci n’avanceront jamais ainsi, c’est une mécanique vaine.
- Il faut garder la place de l’intuition, et ne pas penser que même muni d’un système d’axiomes parfait, on parviendra à faire avancer les maths de façon automatique.
- Une citation de Henri Poincaré, très grand mathématicien également, mais français, montre très clairement sa position :
« Un naturaliste, qui n’aurait jamais étudié l’éléphant qu’au microscope, croirait-il connaître suffisamment cet animal ? Eh bien ! En Mathématiques, il y a quelque chose d’analogue. d’opérations élémentaires quand on aura examiné ces opérations les unes après les autres et qu’on aura constaté que chacune d’elles est correcte, croira-t-on avoir compris le véritable sens de la démonstration ? »
-
- Hilbert est au contraire passionné par cette quête, et persuadé qu’elle aboutira.
- On doit pouvoir trouver un système parfait, dans lequel tout pourra être démontré ou réfuté.
- Admettant que l’on peut avoir plusieurs modèles, plusieurs mondes derrière un même système d’axiomes, il va même jusqu’à affirmer que l’on pourrait donner d’autres noms aux objets mathématiques sans problème : remplacer par exemple “point” par “bière” et “droite” par “table”, et affirmer que par deux bières, il passe une et une seule table.
- Pourquoi pas ? Tant que la cohérence de l’ensemble « définitions/Postulats/démonstration » n’est pas atteint, ce n’est pas gênant. La seule chose qui compte, c’est la validité relative des enchaînements de propositions.

Tombe de David Hilbert à Göttingen avec l’épitaphe:
Wir müssen wissen
Wir werden wissen (source: Wikipédia)
Plein d’optimisme, il lança un jour à la communauté mathématique une phrase restée célèbre: « Wir müssen wissen, wir werden wissen » : « nous devons savoir, nous saurons », phrase qui fut carrément gravée comme épitaphe sur sa tombe…
On peut penser que Cantor avait aussi remarqué ce problème mais Bertrand Russell en a fait la mauvaise publicité en le dévoilant à tout le monde .
- Vers 1900, Russell découvre une incohérence dans la théorie de Cantor : cette théorie permet de créer l’ensemble E des ensembles qui ne se contiennent pas.
Soit E ∉ E et E ne se contient pas, donc par définition E ∈ E , soit E ∈ E et E se contient, donc E ∉ E .
Dans les deux cas il y a contradiction. Selon Gödel c’est bien Russell qui a détecté qu’il y avait une crise sérieuse..
- Le désastre détecté par Russell dans la démonstration de cette preuve de Cantor était que tous les ensembles qui étaient membres d’eux-mêmes étaient exclus de la partie cruciale de la preuve.
Il paraissait donc raisonnable de considérer tous les ensembles qui n’étaient pas membres d’eux-mêmes pour définir un ensemble, mais si on se pose la question à savoir si l’ensemble de tous les ensembles qui ne sont pas membres d’eux-mêmes y est ou non et quoiqu’on suppose, on obtient toujours l’opposé !
C’est une contraction comme celle qui dit « cette assertion est fausse ».
L’ensemble de tous les ensembles ne se contenant pas eux-mêmes est contenu dans lui-même si et seulement si il n’est pas contenu en lui-même.
Alors est-ce que cela signifie que la façon de définir les ensembles est mauvaise ou est-ce que c’est l’ensemble universel qui nous laisse perplexe ?
Et qu’y a-t-il donc de mauvais dans l’ensemble universel ?
Ou bien il y aurait peut-être bien un problème plutôt avec la théorie des ensembles.
On doit à Bertrand Russell d’avoir aidé à reconnaître qu’on était en pleine crise et que les méthodes de raisonnement qui semblaient à première vue parfaitement légitimes dans certains cas conduisaient vers un désastre flagrant, vers des contradictions.
Il eut des paradoxes principalement cités par Russell : celui que l’on vient de mentionner, le paradoxe de Berry,
- Le paradoxe de Berry a été formulé par Bertrand Russell en 1906. On le trouve dans un article, paru en français cette même année, de la Revue de métaphysique et de morale. Russell introduit, dans une discussion à propos du paradoxe de Richard, le « plus petit entier non nommable en moins de dix-huit syllabes qui paraît être ainsi nommé en dix-sept syllabes », et attribue cette définition paradoxale à un bibliothécaire londonien, G. G. Berry.
Le paradoxe de Burali-Forti.
En Résumé, nous sommes donc bel et bien en pleine crise et l’un des personnage centraux de cette crise est Bertrand Russell.
Il faut que quelqu’un vienne à la rescousse. Et c’est là que David Hilbert entre en scène.
David Hilbert
Hilbert enseigne d’abord à Koninsberg puis à Gottingen où il finira sa carrière.
Les 23 problèmes de Hilbert
En 1900, Hilbert a fait un tour d’horizon des mathématiques, définissant ses fameux 23 problèmes. Il a été le mathématicien qui a le plus influencé la formation des mathématiques au XXe siècle et ceci plus que toute autre personne.
Hilbert a décrit 23 problèmes ou questions qui, selon lui, porteraient les mathématiques à un nouveau niveau s’ils étaient correctement résolus.
La liste, a-t-il dit, n’était pas censée exclure d’autres problèmes, il s’agissait simplement d’un échantillon de problèmes.
Échantillon ou pas, depuis que Hilbert a posé pour la première fois les 23 problèmes, un énorme travail a été fait pour trouver les réponses.
Les mathématiciens ont résolu certains des problèmes en quelques années, et d’autres plus tard, mais certains restent non résolus.
Plus de cent ans après que Hilbert les ait répertoriés pour la première fois, une nouvelle lumière brillante brillerait sur les mathématiques si les problèmes restants pouvaient être résolus.
Les grands problèmes non résolus identifiés par Hilbert sont :
- L’hypothèse de Riemann
- L’extension du théorème de Kronecker-Weber
- Le problème de la topologie des courbes et des surfaces algébriques
En mathématiques, l’hypothèse de Riemann est une conjecture formulée en 1859 par le mathématicien allemand Bernhard Riemann, selon laquelle les zéros non triviaux de la fonction zêta de Riemann ont tous une partie réelle égale à 1/2. Sa démonstration améliorerait la connaissance de la répartition des nombres premiers et ouvrirait des nouveaux domaines aux mathématiques.
La fonction zêta de Riemann est définie pour tous les nombres complexes s de partie réelle strictement supérieure à 1 par:
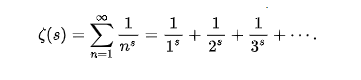
Le théorème de Kronecker-Weber établit en théorie algébrique des nombres le résultat suivant : toute extension abélienne finie du corps ℚ des rationnels, c’est-à-dire tout corps de nombres dont le groupe de Galois sur ℚ est abélien, est un sous-corps d’une extension cyclotomique, i.e. d’un corps obtenu en adjoignant une racine de l’unité aux nombres rationnels.
Ce théorème a été énoncé par Kronecker en 1853. Sa proposition de preuve était incomplète. Weber en 1886 proposa une nouvelle preuve, qui présentait encore une lacune. Hilbert le montra en 1896 en utilisant des méthodes différentes de celles de ses prédécesseurs, et posa le problème de sa généralisation
. Le théorème est aujourd’hui habituellement démontré comme une conséquence de la théorie des corps de classes.
Cependant, il peut aussi être déduit de l’assertion analogue sur les corps de nombres p-adiques : si p est un nombre premier, et K/ℚp est une extension abélienne finie, alors K est inclus dans une extension cyclotomique de ℚp
Développer une topologie des courbes et des surfaces algébriques.
Ce problème comporte deux parties. La première concerne le nombre de branches réelles d’une courbe algébrique, et leur disposition ; de nombreux résultats modernes (Petrovskii, Thom, Arnold) apportent des informations à leur sujet.
La seconde partie du problème pose la question de l’existence d’un nombre maximal de cycles limite pour une équation différentielle linéaire définie par des polynômes homogènes de degré donné ; cette question est encore ouverte.
 C’est dès ses 28 ans qu’il publie son premier résultat important, la résolution du problème de Gordan en théorie des invariants.
C’est dès ses 28 ans qu’il publie son premier résultat important, la résolution du problème de Gordan en théorie des invariants.
Dans sa preuve “non constructiviste”, Hilbert étudie en fait les choses de manière très générale, très abstraites.
Il prend un jeu d’hypothèses, certes respectées par les invariants mais aussi par plein d’autres objets et on n’a finalement pas besoin de préciser ce qu’ils sont et il en déduit des propriétés dont celle finalement qui fait le sujet de l’article.
En fait, sa théorie est beaucoup plus générale et le résultat sur les invariants n’en est qu’une petite partie, tellement annexe qu’elle ne porte pas le nom de théorème mais de “lemme” ce premier résultat important porte déjà la plupart des marques de Hilbert.
D’abord son coté “bulldozer”, à savoir qu’il s’intéresse à un domaine et résout tout ce qu’il y avait à résoudre.
Ensuite, sa résolution ouvre, comme souvent, nombre de nouvelles questions et champs mathématiques.
Enfin, il raisonne en toute abstraction, sans forcément nécessiter un certain lien avec le “réel”.
En somme, Hilbert ne s’intéresse pas à ce que sont les objets “droite” et “plan”, il s’intéresse seulement aux propriétés qu’ils respectent.
Le fait de savoir s’ils “existent”, s’ils sont représentatifs de notre monde ne l’intéresse pas pour construire son axiomatique.
Il se contente alors pour seule définition :
“Nous pensons trois systèmes différents de choses. Nous nommons les choses du premier système les points […].
Nous nommons droites les choses du deuxième système […]. Nous appelons plans les choses du troisième système. […].
Entre les points, les droites et les plans, nous imaginons certaines relations que nous exprimons par des expressions telles que ”être sur“, ”entre“, ”congruent“.
La description exacte et appropriée au but des mathématiques de ces relations est donnée par les axiomes de la géométrie ».
Cela tranche tout particulièrement avec Euclide qui définit d’abord point et droite avant de poser ses axiomes.
Axiomatisation de la géométrie
Extrait des éléments d’Euclid dans l’édition d’Olivier Byrne (sans aucun doute la plus belle édition que vous pourrez trouver)
Les axiomes d’Euclide ne conviennent plus aux mathématiciens de cette époque, en particulier, ils acceptent mal l’axiome des parallèles, qui affirme que par un point extérieur à une droite, ne passe qu’une droite parallèle.
autres et beaucoup sont persuadés qu’il découle
Extrait des éléments d’Euclid dans l’édition d’Olivier Byrne .
Cet axiome parait bien compliqué au regard des autres. En cherchant à démontrer qu’une géométrie où cet axiome est faux ou absurde, ils se retrouvent à créer des géométries certes étranges mais tout à fait cohérentes.
Pire encore, Klein parvient à établir une construction qui démontre que s’il existe une incohérence dans sa géométrie non euclidienne, on peut trouver une incohérence similaire dans la géométrie euclidienne : aucune des deux n’est plus cohérente que l’autre!
Avec Hilbert, un axiome n’est plus vrai car il traduit l’expérience mais car il s’inscrit dans un système consistant. Cela marque le début des mathématiques modernes et marque aussi un point de rupture avec les autres sciences dont on a souvent eu l’occasion de discuter ici.
Ce changement a aussi une autre implication, en tuant le lien avec l’expérience, le problème de l’axiomatisation deviens un problème mathématique et, au même titre que les autres problèmes mathématiques, il pourra être étudié et mener à des démonstrations tel que le théorème de Gödel.
-
Problème de Gordan
 En mathématique, une fois un repère défini, on utilise souvent une équation pour représenter une courbe. Si l’on change de repère, l’équation change alors que l’on a toujours à faire à la même courbe. La théorie des invariants consiste justement à étudier ce qui ne change pas en changeant de repère, les caractéristiques propres de la courbe en somme. En 1868, Gordan montre un premier résultat important dans ce domaine et pendant 20 ans, personne ne parviens à aller plus loin jusqu’à ce qu’Hilbert publie ses résultats. Si le résultat fait polémique à l’époque, ce n’est pas tant pour son résultat ( qui vaudra à Hilbert d’entrer de manière fracassante sur la scène mathématique) mais plutôt pour l’originalité que prend ce résultat (C’est une démonstration d’existence pure ).
En mathématique, une fois un repère défini, on utilise souvent une équation pour représenter une courbe. Si l’on change de repère, l’équation change alors que l’on a toujours à faire à la même courbe. La théorie des invariants consiste justement à étudier ce qui ne change pas en changeant de repère, les caractéristiques propres de la courbe en somme. En 1868, Gordan montre un premier résultat important dans ce domaine et pendant 20 ans, personne ne parviens à aller plus loin jusqu’à ce qu’Hilbert publie ses résultats. Si le résultat fait polémique à l’époque, ce n’est pas tant pour son résultat ( qui vaudra à Hilbert d’entrer de manière fracassante sur la scène mathématique) mais plutôt pour l’originalité que prend ce résultat (C’est une démonstration d’existence pure ). - Dans sa preuve “non constructiviste”, Hilbert étudie en fait les choses de manière très générale, très abstraites. Il prend un jeu d’hypothèses, certes respectées par les invariants mais aussi par plein d’autres objets et on n’a finalement pas besoin de préciser ce qu’ils sont et il en déduit des propriétés dont celle finalement qui fait le sujet de l’article. En fait, sa théorie est beaucoup plus générale et le résultat sur les invariants n’en est qu’une petite partie, tellement annexe qu’elle ne porte pas le nom de théorème mais de “lemme”.
Au contraire du grand mathématicien Français, Poincaré, Hilbert le grand mathématicien Allemand aimait la théorie des ensembles. Hilbert eut donc l’idée de résoudre une fois pour toute tous ces problèmes.
La façon de faire de Hilbert, c’est dire l’utilisation de l’axiomatique remonte donc à l’origine, en fait, à Euclide avec ses fameux postulats.
Hilbert ne l’a pas inventé. Mais il y a ajouté un pas significatif de plus.
Hilbert :Méthode Axiomatique Formelle
 Hilbert dit qu’il faut utiliser toute la technique de la logique symbolique, dont beaucoup de ses collègues mathématiciens étaient partie prenante soit comme utilisateurs soit comme inventeurs, et proposait d’aller aux conséquences ultimes de l’utilisation d’une telle logique symbolique.
Hilbert dit qu’il faut utiliser toute la technique de la logique symbolique, dont beaucoup de ses collègues mathématiciens étaient partie prenante soit comme utilisateurs soit comme inventeurs, et proposait d’aller aux conséquences ultimes de l’utilisation d’une telle logique symbolique.
Puisque ce qui jette le trouble et la contraction en mathématique avec la théorie des ensembles est l’utilisation de mots et que les mots peuvent être très vagues, Hilbert propose un ensemble fini d’axiomes et un langage artificiel pour faire des mathématiques.
C’est ceci qui est l’idée du formalisme.
Formalisme quand tu nous tiens
-
- En poussant le formalisme à sa limite et en inventant un langage complètement artificiel avec des règles du jeu extrêmement précises, Hilbert pensait éliminer tous ces problèmes comme ceux détectés par Russell.
Le paradoxe de Russell
Le paradoxe de Russell, ou antinomie de Russell, est un paradoxe très simple de la théorie des ensembles (Russell lui-même parle de théorie des classes, en un sens équivalent), qui a joué un rôle important dans la formalisation de celle-ci. Il fut découvert par Bertrand Russell vers 1901 et publié en 1903. Il était en fait déjà connu à Göttingen, où il avait été découvert indépendamment par Ernst Zermelo, à la même époque, mais ce dernier ne l’a pas publié.
Énoncé du paradoxe
On peut formuler le paradoxe ainsi : l’ensemble des ensembles n’appartenant pas à eux-mêmes appartient-il à lui-même ? Si on répond oui, alors, comme par définition les membres de cet ensemble n’appartiennent pas à eux-mêmes, il n’appartient pas à lui-même : contradiction. Mais si on répond non, alors, il a la propriété requise pour appartenir à lui-même : contradiction de nouveau.
On a donc une contradiction dans les deux cas, ce qui rend l’existence d’un tel ensemble paradoxal.
- C’était un véritable programme très ambitieux..
- Hilbert ajoutait, et c’est l’une des contributions majeures de son apport :ces règles doivent être si précises que l’on pourrait avoir un vérificateur mécanique de ces preuves. Donc il est complètement certain, objectif et mécanique que la preuve obéit ou non uniquement aux règles. Il ne doit pas y avoir d’élément humain, d’élément subjectif et il n’est pas question d’interpréter.
Si on déclare qu’on a une preuve, on doit pouvoir voir la preuve et la vérifier de façon absolument très claire, de façon mécanique : ou la preuve obéit aux règles, et on a un théorème, ou bien la preuve a une erreur et c’est un échec.
C’était donc l’idée que, pour les mathématiques, un objet ne pouvait être que noir ou blanc.
Noir ou Blanc
On le sait, le mondes réel est plus compliqué et on peut penser légitiment que s’il y a un seul endroit où les choses peuvent véritablement être claires ce serait à coup sûr le domaine des mathématiques pures.
C’est en quelque sorte ce que Hilbert disait quand il proposait cet objectif de formalisation de toute la mathématiques pour en éliminer tous les problèmes.
Mais, c’était un programme et non quelque chose à faire à la va vite en un Week-end.
Hilbert proposait cela comme un objectif à atteindre pour mettre les mathématiques sur des fondations solides.
Lui et d’autres brillants collaborateurs comme un certain John Von Neumann se sont attachés à ce labeur un certain temps, une bonne trentaine d’année, et semblaient très encouragés dans cette voie.
Hilbert ne s’est pas qu’intéressé aux maths. Il se tourne vers la physique dès 1912 pour présenter une théorie cinétique des gaz. Il considère qu’il faut faire une axiomatisation de la physique et pense que cela dit être fait par un mathématicien car il pense que maintenant “la physique est trop difficile pour des physiciens”. Ici comme souvent, il n’invente quelque chose de fondamentalement nouveau mais le simplifie et unifie plusieurs théorie utilisées à l’époque dans l’esprit d’une phrase qu’il prononça dans sa conférence de 1900 : “Une théorie mathématique n’est pas terminée tant qu’on ne l’a pas rendue si claire que l’on puisse l’expliquer à la première personne qui passe dans la rue!”.
 Introduction à la Mécanique Quantique Introduction à la Mécanique Quantique |
Il n’hésite pas non plus à dire qu’après avoir réformé les mathématiques, il s’attaque à la physique et quand il en aura fini il s’attaquera à la chimie qui à l’époque était, selon ses mots, “comme faire de la cuisine dans une école pour filles”. En 1915, il produira une théorie de la relativité et il a eu une influence indirecte déterminante pour l’essor de la mécanique quantique. Il se trouve que les outils mathématiques de la mécanique quantique sont une application directe de la théorie des équations intégrales.
Et puis il eut un tout petit pépin.
- Le pépin c’est d’abord Kurt Gödel en 1931 et puis Alan Turing en 1936.
- Kurt Gödel en 1931
- Alan Turing en 1936
Ils ont simplement montré que la formalisation complète des mathématiques était impossible parce qu’il y avait des obstacles fondamentaux à cela.
Rendre la mathématique transparente comme du cristal où toute chose serait ou Noire ou Blanche était absolument impossible.
Il faut se souvenir en effet que Hilbert avait réclamé une formalisation des mathématiques telle que n’importe qui sur la planète Terre puisse reconnaître si la preuve est soit correcte soit non-correcte.
Noir ou Blanc.
Les règles du jeu doivent être absolument explicites, il doit être utilisé un langage artificiel et les mathématiques doivent donner la vérité absolue.
- C’est en tous cas ce qu’impliquait la proposition de Hilbert.
- Gödel a choqué en montrant que cela ne marcherait pas en 1931.
- Quant à Alan Turing il y est allé plus loin peut-être.
- Résumons schématiquement ce qu’ils ont fait en commençant par Gödel.
- Gödel part de la proposition « cette proposition est fausse » donc ce que je dis est un mensonge.
Si je suis un menteur et que c’est un mensonge je dis donc vrai !
Donc la proposition « cette proposition est fausse » est fausse si et seulement si elle est vraie et il y a donc un problème.
Gödel a en fait considéré la proposition « cette proposition est indémontrable ».
« cette proposition est indémontrable »
Ici indémontrable veut dire indémontrable à partir des axiomes du système axiomatique formel de Hilbert, indémontrable donc avec le système que Hilbert essaye de créer.
Maintenant pensons à une proposition qui dit qu’elle est improuvable.
Il y a deux possibilités : c’est démontrable ou ce n’est pas démontrable.
Supposons donc vraie la proposition ce n’est pas démontrable et qu’il y a donc moyen de le montrer avec le système de Hilbert.
Ceci demande beaucoup de perspicacité : Numérotation de Gödel, construction d’une proposition qui se réfère à elle-même indirectement, parce les pronoms cette ou je ne se trouvent pas directement dans les formules mathématiques .
Donc il y a deux possibilités ou c’est démontrable ou ce n’est pas démontrable. Au sens, donc, que Hilbert a proposé.
Si c’est démontrable, et la proposition dit qu’elle est non démontrable, nous avons prouvé quelque chose de faux .
Ce qui n’est pas très bien.
Et si c’est non démontrable et la proposition dit qu’elle est non démontrable donc elle a dit vrai , vrai que cela soit non démontrable, nous tombons dans un trou.
Au lieu de prouver quelque chose de faux nous avons l’incomplétude.
Nous avons une proposition vraie que notre système formel ne parvient pas à formaliser.
Alors donc ou bien nous sommes en train de prouver des assertions fausses ce qui serait terrifiant ou bien nous sommes en présence d’une chose moins satanique mais néanmoins inattendue, c’est que notre système formel est incomplet. Nous avons quelque chose de vraie mais nous ne pouvons pas le prouver dans notre système. Ainsi donc l’objectif de la formalisation une fois pour toute de toute la mathématique tombe à l’eau.
- Résumons
- L’incomplétude des systèmes formels
- Indiquons le schéma d’intervention autour duquel Gödel a bâti son fameux théorème
- 1) Comment construire une formule arithmétique G représentant l’énoncé suivant:
» La formule G n’est pas démontrable » ?
G est vraie ssi elle n’est pas démontrable, G dit quelque chose d’elle même , elle est autoréférentielle donc source de paradoxes.
2) Gödel montre que G est démontrable ssi sa négation non G est démontrable.
Si G et non G sont démontrables, l’arithmétique est inconsistante. Si l’arithmétique est consistante , alors ni G , ni non G ne sont démontrables. G est une formule indécidable.
3) Bien que G ne soit pas démontrable, elle est arithmétiquement vraie.
4) Puisque G est vraie et qu’elle est indécidable, alors les axiomes sont sémantiquement incomplets . Donc il y a des formules vraies qui ne sont pas décidables au sein du système.
5) Gödel construit une formule A qui représente la proposition » l’ arithmétique est consistante ». - Si A alors G
- A implique G est démontrable, or A n’est pas démontrable dans le système. Si A était démontrable, alors G le serait aussi ; donc la formule est indécidable.
- Ainsi, si l’arithmétique est consistante, alors on ne peut prouver dans l’arithmétique la formule qui exprime cette consistance
Un exemple de formalisation
On dispose un nombre n d’allumettes sur une table. Les joueurs A et B jouent
chacun leur tour et peuvent retirer de 1 à 3 allumettes du tas. Le joueur qui retire la dernière allumette a gagné.
Exemple de partie
On dispose 10 allumettes. C’est au joueur A de commencer.
- Le joueur A retire 2 allumettes, il en reste 8
- Le joueur B retire 1 allumette, il en reste 7
- Le joueur A retire 3 allumettes, il en reste 4
- Le joueur B retire 2 allumettes, il en reste 2
- Le joueur A retire 2 allumettes, il n’en reste plus, le joueur A a gagné.
- Le système formel
Afin de bien mieux comprendre le système formel en question, nous ferons souvent
référence au parallèle avec le jeu des allumettes.
Néanmoins, il doit être bien compris que le système formel en lui même n’a aucun sens.
C’est nous qui choisissons de lui en attribuer un, qui signifie quelque chose pour nous.
- Les formules
Le vocabulaire de notre système sera les lettres A,B et les nombres entiers.
Une formule correcte de notre système sera de la forme : « lettre lettre entier ».
Par exemple, AB14 et BB3 sont des formules bien formées, alors que 4B12 n’est pas une formule.
On peut trouver une signification à ces formules. Convenons que la formule AB12 signifie le joueur A peut gagner de façon sûre si c’est au joueur B de jouer et qu’il reste 12 allumettes.
De la même façon, la formule BB6 signifiera : le joueur B peut gagner de façon sûre si c’est au joueur B de jouer et qu’il reste 6 allumettes.
Chacune de ces formules peut être vraie ou fausse. Nous verrons plus loin que la formule AA10 est vraie.
En effet, le joueur A peut gagner de façon sûre si c’est à lui de jouer et qu’il reste 10 allumettes. Par contre, la formule AA8 est fausse, car le joueur 1 ne peut pas gagner de façon sûre si c’est à lui de jouer et qu’il reste 8 allumettes.
- La négation des formules
Dans ce jeu, les formules ont une négation. Cela signifie qu’à toute formule on peut en associer une autre de façon à ce que si l’une est fausse, l’autre soit vraie et inversement.
En effet, pour une position donnée (un nombre d’allumettes x et le nom du joueur (A ou B) qui va jouer), un des deux joueurs a forcément la possibilité de gagner. Ainsi, si ABx est vraie c’est que BBx est fausse, et si AAx est fausse c’est que BAx est vraie.
- Les règles d’inférence
Comment déduire d’une formule vraie une autre formule vraie ? On voit bien que si AB16 est vraie, alors AA17 l’est aussi, car : Si A gagne alors que c’est à B de jouer et qu’il reste 16 allumettes, alors A gagne aussi si c’est à lui de jouer et qu’il en reste 17 (car il lui suffit d’en enlever une).
- Voici la liste des règles d’inférence de notre système (n remplace n’importe quel entier):
- ABn => AAn+1
- ABn => AAn+2
- ABn => AAn+3
- ABn => ABn+4
- BAn => BBn+1
- BAn => BBn+2
- BAn => BBn+3
- BAn => BAn+4
- Les Axiomes
Nous devons trouver les vérités de base de notre système.
On peut les choisir arbitrairement, mais si on veut obtenir des formules qui signifient toujours quelque chose par rapport au jeu, il faut que nos axiomes soient vrais dans le jeu : AB4 et BA4 sont de bons axiomes, effectivement vrais dans le jeu, car le joueur A gagne forcément si c’est au joueur B de jouer et qu’il reste 4 allumettes et de même le joueur B gagne forcément si c’est au joueur A de jouer et qu’il reste 4 allumettes.
- Testons notre théorie
Partant des axiomes et du système formel, on peut déduire un certain nombre de formules.
Par exemple, AB4 et vrai (c’est un axiome) donc AA5 est vraie aussi (en utilisant la règle
1), AB8 est vraie aussi (en utilisant la règle 4). On peut aussi enchaîner les règles : BA4 => BA8 => BB10
Avec nos 2 axiomes de base, et nos 8 règles d’inférence, nous pouvons ainsi déduire
plusieurs formules (théorèmes), qui nous donnent pour l’ensemble des configurations de plus de 4 allumettes le nom du joueur gagnant.
- L’ordinateur démontre tout
À l’aide d’un ordinateur, on peut s’affranchir du côté mécanique du système formel pour qu’il applique systématiquement les 8 règles à l’ensemble des théorèmes lorsque c’est possible.
Partant des 2 axiomes de base, et en appliquant les règles applicables à chacun d’eux, il démontre les 8 formules suivantes : AA5, AA6,AA7, AB8, BB5, BB6, BB7, BA8
Puis en réappliquant les règles (quand c’est possible) à nos 8 nouveaux théorèmes, la machine peut démontrer 8 nouveaux théorèmes, et ainsi de suite, car le processus ne s’arrête jamais.
- Consistance, complétude…
Nous avons vu que les formules possédaient des négations. la négation de AA5 (notée non(AA5)) est BA5. En effet, soit l’un soit l’autre des joueurs a la possibilité de gagner de façon sûre dans n’importe quelle configuration. Choisissons une formule (par exemple AB7654) de notre système, et attendons infiniment longtemps (en théorie) pour voir si l’ordinateur la démontre. Quatre cas peuvent se présenter :
- Il démontrera AB7654 et pas BB7654 (la négation de AB7654)
- Il démontrera BB7654 , et pas la formule AB7654
- Il démontrera la formule AB7654 et la formule BB7654
- Il ne démontrera ni AB7654 , ni BB7654
Les 2 premiers cas ne posent pas de problème. En revanche, si le troisième se présentait nous pourrions dire que le système est inconsistant. En effet, il permet de démontrer une chose et son contraire.
Il est bien évident que dans toute configuration (ici B7654) il est impossible que les 2 joueurs aient une stratégie gagnante à la fois…
Le quatrième cas pose aussi un problème. Si vous étudiez mieux le jeu, vous verrez facilement que dans toutes configuration, un des joueurs a une stratégie gagnante.
Par conséquent, nous savons que soit AB7654, soit BB7654 est vraie (en l’occurrence, c’est AB7654).
Si le quatrième cas se présentait, nous pourrions dire que le système formel est incomplet, car il existerait certaines vérités qu’il ne permet pas de démontrer.
Bien entendu, dans notre exemple simple, le système est en fait consistant et complet, c’est à dire qu’il ne permet pas de démontrer une chose et son contraire, et qu’il permet de démontrer toutes les formules qui sont vraies.
Mais il n’en est pas de même pour tous les systèmes. Le travail de Gödel a consisté à démontrer que dans les systèmes formels suffisamment complexes pour contenir l’arithmétique :
on ne peut pas simplement démontrer la consistance ;
.si le système formel est consistant, alors il est incomplet
Maintenant on peut très bien se douter que Hilbert ne voulait pas réellement une formalisation de toute la mathématique. Il n’a pas dit qu’il fallait que tous les mathématiciens devaient obligatoirement travailler dans un langage artificiel en produisant des preuves formelles.
Les preuves formelles tendent à devenir très longues, inhumaines et très difficiles ne serait-ce qu’à lire .
On doit peut-être penser que l’objectif réel de Hilbert était plus philosophique.
Si on croit que la mathématique doit délivrer la vérité absolue, alors on peut croire que Hilbert avait raison et que l’on devait trouver une façon de formaliser une fois pour toute toute la mathématique. C’est ceci qu’essaye de faire la logique mathématique, c’est ceci qu’essaye de faire la méthode axiomatique qui une idée consistant à éclater les preuves en des preuves de plus en plus petites.
Leibnitz croyait à cela.
Boole le pensait.
Frege et Peano et Russell et Whitehead en étaient convaincus.
C’est l’idée de rendre très clair comment la mathématique opère pas après pas.
Et cette idée sonnait plutôt juste.
Malheureusement arrivé en ce point tout est tombé à l’eau.
On peut lire témoignage de ce choc chez Hermann Weyl ou chez Von Neumann .
Il existe des textes où on peut lire leur grand désarroi à travers des confessions de ce type: je suis devenu mathématicien car c’était ma religion, je croyais en la vérité absolue, là était la beauté, le monde réel était affreux, mais je me suis réfugié dans la théorie des nombres. Et tout à coup Gödel a surgit et a ruiné toute chose et je veux me tuer.
Bon tout cela est délicieusement angoissant . Cependant cette
« cette proposition est non démontrable » est une assertion qui semble bien étrange. Il y a bien des façons de rationaliser et assurément l’être humain est très bon à ce petit jeu ne serait-ce que pour ne pas se retrouver face à des réalités déplaisantes. On pourrait croire que ces réalités déplaisantes peuvent facilement se contourner : il suffirait seulement de dire, mais enfin qui donc s’en préoccupe : les assertions normalement utilisées en mathématique n’ont pas cette forme. C’est un non-sens et une stupidité totale d’aller dans ce genre de direction. Mais ceci n’est qu’une incantation car Gödel a fait de « cette proposition est non-démontrable » une assertion élémentaire de la théorie des nombres .
Bien sûr, dans sa forme originale elle paraît être un non-sens.
Qui, en effet, a jamais entendu dire qu’une assertion en mathématique dit d’elle-même qu’elle est non-démontrable ?
Mais en fait Gödel transforma cette proposition en une assertion numérique élémentaire de la théorie des nombres, en arithmétique.
Cela devient une assertion d’un énorme volume, qui de façon très astucieuse, implique la numérotation de Gödel de toutes les assertions utilisant les entiers premiers.
Elle est donc récrite de telle façon à ressembler à une assertion mathématique réelle.Mais elle se réfère réellement de façon indirecte à elle-même et dit qu’elle est non-démontrable.
Et c’est pour cela qu’il y a problème.
Mais la plupart des gens ne savaient pas quoi faire de cela. Donc disons que c’était un résultat surprenant où en fait la surprise correspond à un choc terrible.
- Résumons.
1931 Gödel « cette proposition est non-démontrable » surprise.
Puis est arrivé Turing.
1936 Turing
Il commence lui, le premier à parler d’ordinateur.
1936 Turing ordinateur
Turing a dû inventer l’ordinateur puisque Hilbert parlait d’utiliser obligatoirement des procédures mécaniques pour vérifier les preuves mathématiques.
Turing se disait que ce dont Hilbert parlait doit être un programme d’ordinateur pour vérifier les preuves.
Mais d’abord il fallait à Turing spécifier ce qu’était un ordinateur et c’est exactement ce qu’il y a dans sa publication de 1936 et c’est la machine de Turing, à une époque où il n’existait pas d’ordinateur !
On peut dire que c’est de l’invention, sur le papier, de l’ordinateur qu’il s’agit.
Ce que Turing a montré en fait c’est qu’il existe des assertions concrètes qui échappent à la puissance des mathématiques. Actuellement , on pense aux ordinateurs en tant qu’appareils physiques et donc ils ressemblent aux objets physiques. C’est en fait une machine qui va au-delà, c’est une idéalisation du travail physique et nous avons donc cette machine qui marche vraiment et Turing tombe alors sur le problème de son arrêt. - 1936 Turing ordinateur Le problème de l’arrêt
Le problème de l’arrêt dit qu’il n’y a aucun moyen de savoir si, éventuellement, un programme d’ordinateur s’arrêtera.
Actuellement, cela est la chose la plus facile au monde pour décider si un programme s’arrête. On l’exécute et quand on devient fou de rage à force d’attendre, on y est, ça ne s’arrête pas tant que notre rage dure. Qui se préoccupe de la longueur de l’attente.
Mais ce que Turing a montré c’est qu’il y a vraiment un problème si on ne met pas une limite de temps à notre attente. Ceci est de la mathématique très abstraite car dans la vie réelle, il y a toujours une limite de temps.
On ne peut pas exécuter un programme pendant un million d’année, encore moins pendant un milliard d’années et que dire d’un temps de 10 10100 années !
Donc si on met une limite de temps, le problème de l’arrêt est trivialement résolu et se décide facilement toujours en principe : il n’y a qu’à l’exécuter et voir s’il s’arrête ou non avant le temps limite qu’on s’est donné.
Mais si on ne se donne plus de temps limite, il n’y a aucune solution.
Il n’y a pas moyen de décider à l’avance si un programme d’ordinateur va s’arrêter ou non. Il en découle alors qu’il n’existe aucun ensemble mathématique d’axiomes au sens de Hilbert capable de prouver qu’un programme d’ordinateur s’arrête ou non.
- Car si on pouvait prouver qu’un programme s’arrête ou non, alors ceci implique qu’on peut exécuter toutes les preuves possibles rangés par ordre de longueur et vérifier qu’elles sont correctes et éventuellement soit trouver une preuve que le programme va s’arrêter ou trouver une preuve qu’il ne va pas s’arrêter.
- Actuellement et en pratique, exécuter toutes les preuves possibles exige une quantité de temps astronomique. Imaginons combien, déjà, il y a de preuves de la longueur d’une seule page seulement ! On ne peut en arriver au bout ! Mais en principe conformément au système axiomatique formel de Hilbert on peut exécuter toutes les preuves possibles rangées par ordre de taille et s’assurer qu’elles vérifient ou non les règles. Donc si on dispose d’une axiomatisation formelle des mathématiques qui nous permette de prouver qu’un programme s’arrête ou non cela donnerait justement une procédure mécanique en exécutant toutes les preuves possibles rangées par ordre de taille et de décider si un programme s‘arrête ou non.
- Turing a montré qu’on ne peut pas faire cela.
- Sa preuve utilise l’argument diagonal de Cantor.
Toutes ces idées sont connectées entre elles.
On voit que le travail de Turing trace les limites des mathématiques de façon plus naturelle parce qu’il est question d’un appareil physique, d’un ordinateur. - 1936 Turing ordinateur Problème de l’Arrêt naturel
On peut fantasmer un peu et transformer notre ordinateur physique en une machine théorique .
Il suffit d’imaginer un ordinateur qui ne tombe jamais en panne, qui peut exécuter indéfiniment des instructions et qui possède des moyens de stockage aussi grands qu’il le souhaite de sorte que si les nombres deviennent trop grands il peut néanmoins continuer à calculer (remarquons au passage que c’est exactement vers ce genre de performances que tend toute la technologie des ordinateurs (et partant, toute la technologie tout court) à des coûts de plus en bas et donc de plus en plus réalisables et généralisables – on pourrait même risquer de dire que la course aux performances est une théorisation de la réalité-).
Les limites détectées par Turing apparaissent plus sérieuses et plus dangereuses que celle découvertes par Gödel
Oups ! Une machine formelle à poser et à résoudre tous les problèmes ?
- Tout est déjà là, dés le début, en 1936.
L’invention de l’ordinateur est une réponse à un argument théorique fou.
On n’a certes pas en jeu les milliards de dollars de la technologie en 1936 , mais les jeux sont faits, tout est posé, à l’état embryonnaire bien sûr, dans cet article de 1936 !
Von Neumann lui, l’avait vu : la machine universelle de Turing s’identifie à la machine programmable capable de prendre en charge par le calcul n’importe quel problème .
Il existait, bien sûr, déjà bien avant Turing des machines à résoudre des problèmes par le calcul, mais ces machines ne prenaient en charge par le calcul qu’un type très spécifique de problèmes.
Ce n’est pas pour rien que John Von Neumann eut l’idée du logiciel et fut le premier programmeur de l’histoire de l’informatique, il a su voir cette flexibilité, cette notion potentielle d’universalité du calcul de la machine de Turing. - Toute la Technologie est là, en condensé.
Et, en fait, Gödel comme on l’a dit précédemment utilisait dans la démonstration de son fameux théorème une sorte de LISP où se cache un véritable langage formel, un langage de programmation, quoi !
- Dans le papier de Turing, c’est plus explicitement que le langage de programmation est donné et c’est d’ailleurs un authentique langage machine.
- Bien sûr, maintenant le langage machine est mal vu, un langage dont personne d’équilibré ne voudrait pour programmer.
On peut se rendre compte maintenant que si Turing avait utilisé un langage plus complexe, il aurait été obligé d’introduire un relais supplémentaire constitué par un manuel minimal d’utilisation de ce langage dans le papier de 1936, et que donc personne n’aurait rien compris à son véritable résultat de calculabilité. - Qu’en est-il actuellement et qui se préoccupe vraiment des problèmes de fond de la mathématique ?
- Hilbert est mort, la II ème guerre est passée et le monde va dans des directions de moins en moins philosophiques. D’ailleurs les questions philosophiques de fond ont tendance à moins intéresser depuis qu’on voit de jeunes morveux devenir milliardaires juste en démarrant des starts-up sur le Web !
- Ce qui est insupportable en fait, c’est que même dans le monde abstrait des mathématiques pures, les mathématiciens eux-mêmes affirment que dans la pratique ils font exactement de la même façon ce qu’ils ont toujours fait, et qu’en définitive tout cela ne s’applique pas aux problèmes qui les préoccupent !
Ce fut typiquement la même réaction à l’époque de Gödel et Turing face à leurs travaux sur l’incomplétude.
Au début ce fut un choc terrible, puis c’est passé à l’autre extrême.
- On dirait de cette amnésie une technique névrotique compensatrice de l’espace mental que Freud a tenté de si bien expliquer.
- Les conséquences de ces résultats sont soigneusement refoulées ou noyées dans un verbiage théologique où l’incantatoire prend si facilement le pas sur le rythme d’un débat qui n’en est pas un.
Et en Physique, que ce passe-t-il?
Vous avez dit méta quoi déjà ?
- Regardons un autre domaine non moins passionnant, la physique.
- Bien que le modèle de Newton soit en progrès significatif par rapport au modèle de Ptolomée, il est insuffisant ou INCOMPLET, dans le sens où le système explicatif déduit du modèle Newtonien n’est pas un espace fermé borné , il existe des trous, i.e. beaucoup de phénomènes physiques ne reçoivent pas d’explication dans le modèle d’Univers de Newton.
- Dans le modèle d’Einstein les vitesses relatives apparaissent de manière plus significative et les concepts qui paraissaient les plus stables éclatent, ainsi ni la masse ni même le temps ne sont invariants et peuvent être vus comme des VARIABLES seule la vitesse de la lumière est déclarée constante dans tout repère d’inertie !
- Si la théorie restreinte reste encore susceptible d’être capturée par notre intuition moyennant un coût de difficulté ne dépassant pas les mathématiques élémentaires, la théorie générale, elle, échappe à notre simple bon sens et à nos raisonnements linéaires car la théorie est en réalité décrite dans un espace géométrique abstrait d’ordre supérieur à 3 où la visualisation intuitive humaine ne peut plus se faire naturellement et où donc des relais abstraits sont nécessaires, pour par exemple, simplement percevoir les données mécaniques d’un problème.
- Les déformations et les distorsions possibles dans cette physique impliquent la maîtrise d’outils mathématiques très puissants comme la manipulation correcte des règles du calcul tensoriel qui ne représentent que le moindre des pré-requis pour accéder à ce langage abstrait capable de décrire les faits de cette physique.
- Actuellement, 4 types de force ont été distingués par les physiciens(- certains physiciens soupçonnent l’existence d’une 5EME force fondamentale.) :
-La gravitation (responsable de la cohésion des astres)
A la fin du XVI siècle, Isaac Newton élabore une loi de la gravitation, force responsable de l’attraction réciproque de corps massifs sous l’effet de leur masse. Il faudra toutefois attendre le XX siècle et Einstein pour en comprendre la nature.
- c’est la force la plus faible –peu sensible à l’échelle des particules à cause de leurs petites masses elle devient sensible à l’échelle macroscopique mais aussi à l’échelle limite de Planck c’est à dire aux ultra très petites dimensions (10–33 cm (la plus petite distance possible selon Planck qui est d’ailleurs parcourue en 10-43 s par la lumière)
- -L’interaction électromagnétique (responsable de la cohésion des molécules)
- -L’interaction faible (responsable de la radioactivité béta (désintégration))
- -L’interaction forte (responsable de la cohésion des noyaux atomiques)
(là encore de douloureux débats épistémologiques ou philosophiques peuvent, avec raison, avoir lieu – pourquoi pas 5 ou 10 ou même 1 seule force fondamentale ? y a-t-il des forces fondamentales encore cachées ?)
- Avant la théorie quantique, les forces se transmettaient à distance par l’intermédiaire d’un mystérieux champ de force émis par les particules.
Après la théorie quantique, les forces ne s’exercent entre deux fermions que s’il y a échange d’une particule médiatrice, appelée boson. Or plus le boson sera lourd, plus l’interaction sera de courte portée. Cette théorie porte le nom indigeste d’électrodynamique quantique.
Dans les années 1920 Thomas Kaluza et Oscar Klein ont tenté d’unifier les interactions électromagnétique et gravitationnelle à partir du formalisme de la relativité générale.
-la théorie de la relativité générale permet d’interpréter la gravitation comme une déformation de l’espace-temps dont la cause est la présence de matière et/ou d’énergie. La gravitation se ramène alors à un phénomène purement géométrique.
-les équations de la relativité générale telles que formulées par A. Einstein ne parviennent pas à fournir une telle description géométrique pour l’électromagnétisme.
Kaluza et Klein ont eu l’idée de rajouter une 5ème dimension à l’espace-temps et de façon surprenante ils parvinrent à un résultat satisfaisant !
Kaluza et Klein proposent d’interpréter cette dimension, que personne n’a jamais observée, comme une dimension «enroulée » sur elle-même en tout point de l’espace dans un cylindre dont le diamètre n’exèderait pas 10 –33 cm (constante de Planck )
L’interaction électromagnétique possède une caractéristique intrinsèque : si l’on modifie globalement partout à la fois, le potentiel électrique, les phénomènes électromagnétiques n’en sont pas affectés.
Modifier globalement le potentiel électrique revient en fait à changer la phase des ondes associées aux particules(phénomène bien connu en électrodynamique classique)
Interaction électromagnétique et symétries
- L’électro-dynamique quantique ou QED
La description quantique de l’interaction électromagnétique a été réalisée dans les années 40 et s’est achevée par une théorie nommée électro-dynamique quantique (ou QED pour Quantum Electro-Dynamics). La QED repose sur la théorie invariante des perturbations, formalisme théorique parachevé par Richard Feynman. La théorie invariante des perturbations est issue de la méthode classique des perturbations élaborée au XIXième siècle pour résoudre le problème à trois corps en mécanique céleste essentiellement.
La loi universelle de la gravitation de Newton donne des résultats très précis lorsque le nombre d’objets impliqués se limite à deux. Pour un nombre d’objet supérieur à deux, la loi de Newton aboutit à des équations qui ne sont pas solubles de façon analytique dans la plupart des cas. C’est ce que l’on appelle de manière générique le problème à trois corps. Les astronomes ont donc mis au point une méthode reposant sur l’idée qu’il est possible de traiter le problème comme un système à deux corps auquel on ajoute de petites perturbations engendrées par le troisième astre. Les équations du mouvement sont alors solubles et des solutions analytiques existent, cependant, cette méthode n’est applicable qu’à la seule condition que le champ du troisième astre soit effectivement beaucoup plus faible que celui des deux autres afin de pouvoir le traiter comme une petite perturbation. Cette méthode a permis à John Couch et Urbain Le Verrier de supposer l’existence de la planète Neptune en étudiant les irrégularités de la trajectoire d’Uranus. Neptune fut effectivement découverte en 1846 par Johann Galle.
- Richard Feynman a étendu cette méthode à l’électrodynamique dans une contexte quantique. Les interactions quantiques sont alors décrites comme des petites perturbations locales du champ électromagnétique. Les résultats ainsi obtenus sont en accord jusqu’à la huitième décimale avec l’expérience, faisant de la QED la théorie la plus exacte que l’Humanité ait jamais conçu. Selon la QED, les interactions électromagnétiques se ramènent à l’échange de photons entre particules chargées. Le photon est donc le quantum de l’interaction électromagnétique. La constante de couplage a la valeur de 1/137. Enfin, la QED est renormalisable, c’est-à-dire qu’il est possible, après des manipulations mathématiques spéciales, d’obtenir une valeur finie pour le calcul des probabilités de diffusion électromagnétique.

Cependant, malgré ses succès retentissants, la QED ne répond pas a une question fondamentale : quelle est la nature profonde de l’interaction électromagnétique ? Un début de réponse à cette question a été donné en abordant la QED sous l’angle des symétries.
- Les symétries de la QED
L’interaction électromagnétique possède une caractéristique qui lui est propre : si l’on modifie globalement, partout à la fois, le potentiel électrique, les phénomènes électromagnétiques ne sont en rien affectés. Ceci montre clairement, que l’interaction électromagnétique est invariante pour des modifications globales du potentiel électrique. En fait, modifier globalement le potentiel électrique revient à changer la phase des ondes associées aux particules. Ce phénomène était déjà bien connu en électrodynamique classique. La phase d’une onde peut être assimilée à un angle dans un cercle. L’invariance des lois de l’électrodynamique par changement global de la phase signifie donc que l’on peut prendre n’importe quel angle comme phase sans affecter pour autant les phénomènes de l’électrodynamique.
Adoptons la démarche de la construction des théories de jauge à savoir, imposons maintenant que la modification locale du potentiel électrique n’affecte pas non plus les lois de l’électrodynamique. En pratique, cette symétrie locale n’est pas observée dans la nature mais nous souhaitons étudier comment l’électrodynamique réagit lorsque celle-ci lui est imposée. Pour illustrer de façon imagée le phénomène, représentons le potentiel électrique en chaque point de l’espace par la phase de l’onde associée, c’est-à-dire par l’angle de cette phase. Dans une région vide de l’espace, cette phase est partout identique. On peut imaginer que les extrémités de chaque segment représentant la phase dans chaque cercle sont reliées les unes aux autres par des ressorts. Dans le cas d’un espace vide, ces ressorts sont au repos et n’exercent donc aucune tension.

Phase en 3 points A, B et C de l’espace
Si l’on procède à un changement global du potentiel, cela revient à modifier partout la valeur de la phase de la même quantité, donc à faire tourner tous les segments d’un même angle. Du coup, après cette opération, les ressorts ne seront toujours pas ni tendus, ni comprimés et n’exerceront donc toujours aucune tension.

Maintenant, modifions localement la phase. Cela revient à tourner le segment d’un angle différent en chaque point de l’espace. A ce moment, les ressorts vont être tendus par endroits, comprimés à d’autres. Ils vont donc exercer une tension en chaque point de l’espace. Cette tension, qui est une force, n’est rien d’autre que la manifestation d’un champ. Ce champ n’existait pas initialement mais il est apparu à partir du moment où l’on a fait varier localement le potentiel électrique, c’est-à-dire la phase.

La description qui vient d’être faite n’est bien sûr qu’une image qui illustre, tant bien que mal, des opérations mathématiques très abstraites. Lorsque l’on étudie de plus près les propriétés du champ qui est apparu après avoir imposé une symétrie locale, on s’aperçoit que ce champ n’est rien d’autre que le champ électromagnétique !!! L’électrodynamique quantique peut donc être interprétée comme une théorie de jauge.
Le champ électromagnétique prend donc son origine dans la symétrie de la nature vis-à-vis du potentiel électrique. L’électrodynamique quantique est symétrique pour toute rotation de l’angle de la phase de l’onde associée à une particule. Les rotations dans un cercle constituent un groupe noté U(1) (Unitaire 1). On se réfère souvent à la théorie de l’électrodynamique quantique par le groupe qui représente l’interaction électromagnétique, c’est-à-dire par le nom cabbalistique U(1).
Selon la théorie de Kaluza-Klein , la symétrie propre à l’électromagnétisme (ou groupe U(1)) serait réalisée dans la 5EME dimension qu’ils ont rajouté. Dans notre espace-temps à 4 dimensions, cette symétrie n’apparaît pas de façon explicite dans les équations de la relativité générale.
La 5ème dimension imaginée par Kaluza-Klein joue donc le rôle de l’espace des phases de l’électromagnétisme.
La symétrie, en physique est une transformation des variables (qui peuvent être des variables géométriques ou plus abstraites) qui ne change pas la formulation des lois physiques- la symétrie selon le sens commun n’est qu’un cas particulier (transformation de x en –x) et qui en physique s’appelle transformation de parité.
Les physiciens ont très vite remarqué que les lois de la nature n’étaient pas modifiées par
-La transformation de Parité (notée transformation P)(c’est l’image miroir des phénomènes observés)
-La transformation par inversion de toutes les charges électriques impliquées dans un phénomène(notée transformation C)
-La transformation par inversion du sens du temps(notée transformation T)
En outre on distingue
-Les symétries globales : la même transformation s’applique partout
-Les symétries locales : la transformation dépend de la valeur de la variable à transformer.
Si la nature est intrinsèquement invariante ou symétrique pour certaines transformations globales, ce n’est, en général pas le cas vis-à-vis des symétries locales.
Maintenant, supposons que nos physiciens ignorent l’existence de la gravitation, mais ils savent que les lois de la nature sont symétriques pour les translations globales dans l’espace et dans le temps. Ils se proposent alors d’étendre cette propriété à une symétrie locale. Pour cela, ils imposent aux lois de la nature d’être invariantes pour des translations locales dans l’espace et dans le temps et injectent donc cette contrainte dans les équations du mouvement. Le résultat qu’ils obtiennent est extraordinaire : un nouveau terme apparaît dans les équations, terme qui décrit une entité qui n’est rien d’autre qu’un champ. En étudiant de plus prés ce champ, ils s’apercevront bien vite que ce champ n’est rien d’autre que la gravitation !
Herman Weyl en 1923 a retrouvé les résultats de la relativité générale en procédant de la sorte.
La gravitation apparaît dans cette nouvelle approche comme une condition à ajouter dans les équations du mouvement pour qu’une symétrie globale(les translations dans l’espace-temps) puissent devenir une symétrie locale.
Une symétrie locale est également nommée une symétrie de JAUGE et les théories bâties sur de telles symétries sont appelées des théories de jauge.
Les travaux de Weyl ont montré que la théorie de la relativité générale était une théorie de jauge.
Pourtant, même cette théorie connaît des TROUS. Alors qu’elle est un système d’explication acceptable à l’échelle Macroscopique, elle ne l’est plus du tout à l’échelon Infra, où pourtant les conditions même qui ont permis son émergence, sont le plus fréquemment réalisées. En effet c’est dans le monde microscopique que l’on a le plus de chance de rencontrer des objets filant à des vitesses proches de celle de la lumière -Einstein aura tout le temps cherché, en vain, une théorie unitaire capable de s’appliquer à tous les champs.
Mais le modèle, sommes toutes, Géométrique sous-jacent à la théorie de la relativité, n’est-il pas finalement une tentative déterministe de reconstruire le stochastique (à la manière de Cournot qui pose le stochastique comme la confluence de plusieurs déterminismes indépendants). Le stochastique ne serait donc pas un concept primitif de cette théorie mais correspondrait plutôt à un effet.
En même temps que se déroulait la crise en mathématique, de façon parallèle une crise courrait en physique depuis les années 1920.La mécanique quantique. Et l’année critique fut l’année 1924.
1924 La Mécanique Quantique
Et c’est toute la question de l’incertain et de l’aléatoire en physique fondamentale.
De même que derrière la lecture de textes sur le théorème d’incomplétude de Gödel on entendait clairement le cri d’angoisse « Oh,mon Dieu ! » de même il y avait des textes sur la physique qui se demandaient ce qu’était devenu le déterminisme en physique, la prédicabilité , est-ce qu’il peut exister l’aléatoire, est-ce que Dieu joue aux dés ?
Et Einstein réponds non , Dieu ne joue pas aux dés.
Il détestait la mécanique quantique. Et tout le monde disait oui, Dieu joue aux dés.
La Mécanique Quantique quant à elle pose le stochastique et propose et manipule des processus non-déterministes qui ne pouvaient que hérisser celui qui a GEOMETRISE la physique.
Plus grave, la porte est ouverte à des systèmes de représentation intégrant de plus en plus de niveaux d’abstraction avec les complexités qui en découlent et la multiplication rhédibitoire des formalismes.
Les physiciens graphiques apparaissent : Louis de Broglie, ménage le choux et la chèvre en déclarant que la matière est à la fois une onde (à la Manière des champions la physique quantique (qui ont introduit un degré d’abstraction supplémentaire dans les sacro-saintes règles de l’observation (interaction de ce qui est observé et de l’appareillage qui observe)) et un corpuscule à la manière des tenants des théories plus classiques .
Nous avons là un cas de rivalité mimétique intéressant
Les 2 théories ont été validées par de nombreuses expériences et ont la prétention d’être des systèmes d’explication universels- mais ces deux théories scientifiques puissantes sont en fait incompatibles l’une avec l’autre :
si la mécanique quantique a raison alors la relativité générale a tord ! ! !
La théorie des quanta
la mécanique de Newton paraissait fournir une description exhaustive des mouvements des corps.
Mais en ce changement du 19ème au 20èmesiècle, de nouvelles observations mirent en lumière ses limites, parmi lesquelles le spectre de la lumière émise par les gaz chauffés ou dans lesquels une décharge électrique a lieu.
Au début du 20èmesiècle, le physicien anglais Ernest Rutherford découvrit la nature des particules alpha et montra qu’elles sont constituées par des noyaux d’hélium, et énonça la loi des transformations radioactives.
Les physiciens avaient aussi à découvrir une interrelation pertinente entre les deux théories de la lumière: la théorie corpusculaire, qui présente la lumière comme un flot de particules, et la théorie ondulatoire, qui la considère comme constituée d’ondes électromagnétiques. Un troisième problème théorique consistait dans l’absence de toute base moléculaire pour la théorie thermodynamique. Dans son livre intitulé les Principes élémentaires de la mécanique statistique (Elementary Principles in Statistical Mechanics, 1902), le physicien américain Josiah Gibbs admit l’impossibilité de développer une théorie de l’action moléculaire capable d’embrasser les phénomènes de la thermodynamique, du rayonnement et les phénomènes électriques tels qu’ils étaient compris à l’époque.
Au tournant du siècle, la nature ondulatoire de la lumière semblait donc confirmée grâce à de nombreuses expérimentations.
L’interférence et la diffraction avaient permis la détermination de la longueur d’onde de la lumière; les phénomènes de polarisation avaient mis en évidence sa transversalité. La confirmation expérimentale de la théorie de Maxwell, grâce aux expériences de Hertz, indiqua qu’elle est constituée d’ondes électromagnétiques. L’interaction entre lumière et matière n’était cependant pas encore élucidée. Certains corps étant transparents, d’autres se laissant traverser seulement par des longueurs
d’onde déterminées, il s’agissait d’expliquer pourquoi le spectre ne présentait pas de continuité. En 1888, Heinrich Hertz remarqua par hasard que les surfaces métalliques (une plaque de zinc, par exemple) émettent des électrons quand elles sont irradiées par des rayons ultraviolets. La libération des électrons est indépendante de l’intensité (ce fut le physicien allemand Philipp Lenard qui en apporta la preuve), mais elle augmente de manière linéaire avec la fréquence de la lumière incidente.
La physique quantique est née avec le 20èmesiècle, en 1900, à la suite des travaux de Max Planck.
Max Planck étudiait le phénomène de « rayonnement des corps noirs ». Selon la théorie classique, les échanges d’énergie à l’intérieur du corps noir s’effectuaient de manière continue. (L’expression corps noir fait référence à un corps idéal, ou surface qui absorbe, sans aucune réflexion, toute l’énergie de rayonnement.) Un corps porté à une haute température («!chaleur rouge!») émet la plupart de ses rayonnements dans la gamme des basses fréquences (rouge et infrarouge)!; un corps porté à une plus haute température (« chaleur blanche ») émet relativement plus de rayonnements à de plus hautes fréquences. Dans les années 1890, les physiciens réalisèrent des études quantitatives détaillées de ces phénomènes et représentèrent les résultats sous la forme d’une série de courbes ou de graphiques. La théorie classique ou préquantique prédisait un faisceau de courbes tout à fait différentes de celles réellement observées Cette théorie prédisait que l’intensité du rayonnement d’un corps noir pour une longueur d’onde donnée était proportionnelle à la quatrième puissance de la valeur de cette longueur d’onde. Ce résultat n’était pas en accord avec les observations expérimentales d’une part, et impliquait que l’énergie totale rayonnée par un corps noir était infinie d’autre part. Il fallait donc réviser en profondeur la théorie.
Max Planck prit le problème à l’envers et tenta de trouver une formulation analytique de la courbe expérimentale observée. Cette formulation obtenue, il lui fallut l’interpréter physiquement. La seule interprétation acceptable qu’il trouva consistait à remplacer les échanges continus d’énergie par des quantités finies qu’il baptisa quanta. La quantité d’énergie transportée par un quantum d’énergie est alors proportionnelle à la fréquence du rayonnement associé. Le rapport de proportionnalité est égal à une constante nommée constante de Planck et représentée par la lettre h
Ainsi, selon la théorie des quanta de Planck, tout échange d’énergie entre quelques corps que ce soit, s’opère par des transferts de quantités d’énergie finies. On dit que les échanges d’énergie sont quantifiés.
Le travail de Planck consista principalement à développer une formule mathématique pour décrire les courbes de façon exacte; il en déduisit alors une hypothèse physique qui pouvait expliquer la formule. Son hypothèse indiquait que l’énergie était rayonnée seulement par quanta d’énergie hu, où u est la fréquence et h le quantum d’action, connu aujourd’hui sous le nom de constante de Planck, que nous retrouvons dans l’équation suivante:
1/2mv²=hf-W h=6,67.10e-34J.s
L’énergie cinétique mv²/2 des électrons est donc indépendante de l’intensité, mais pas de la fréquence f du rayonnement incident!; la constante de Planck h a toujours la même valeur pour tous les métaux et est donc considérée comme une constante universelle. W prend différentes valeurs suivant les matériaux, et si sa valeur est supérieure à hf, la fréquence de la lumière est insuffisante pour libérer les électrons du métal.
La mécanique ondulatoire, l’équation de Schrödinger et le principe de complémentarité
Dès 1905, Albert Einstein interpréta avec succès l’effet photo-électrique à l’aide de la toute jeune théorie des quanta de Planck (Albert Einstein expliqua les résultats obtenus par Lenard en relation avec l’effet photoélectrique (un phénomène observé expérimentalement et au cours duquel les électrons sont émis des surfaces métalliques sur lesquelles on dirige un rayonnement). Il s’agit de l’hypothèse photonique. Einstein écrit, dans son article la Production et la génération de la lumière du point de vue heuristique (1905): « En partant de l’hypothèse que la lumière incidente soit constituée de photons d’énergie hf, on parvient à expliquer l’émission des électrons suite à l’irradiation lumineuse de la manière suivante: les photons pénètrent dans la couche superficielle du corps et leur énergie se transforme, en partie du moins, en énergie cinétique des électrons. Le cas le plus simple est celui dans lequel un photon cède toute son énergie à un seul électron. En outre, pour quitter le corps, chaque électron doit accomplir un certain travail W, caractéristique du corps. Il s’ensuit que l’énergie cinétique des électrons sortants vaut: 1/2mv²=hf – W Cette hypothèse rencontra de vives oppositions, même de la part de Planck, et ce n’est qu’en 1921 qu’Einstein reçut le prix Nobel pour sa théorie sur l’existence des photons, laquelle eut plusieurs confirmations expérimentales). L’idée force de cette interprétation réside dans le fait que le quantum d’énergie associé à une fréquence de lumière se comporte comme une particule de matière. Einstein baptisa ce corpuscule de lumière le photon.
Ce qui est véritablement révolutionnaire dans l’idée d’Einstein tient dans le fait que la lumière avait acquis, avec la théorie de l’électromagnétisme achevée par Maxwell, une nature résolument ondulatoire. La lumière était alors perçue comme une onde électromagnétique. Avec l’hypothèse du photon, la lumière apparut tout à coup comme une entité hybride, se comportant tantôt comme une onde, tantôt comme une particule. L’invention par Einstein du concept de photon fut le premier pas vers une révolution en profondeur des fondements mêmes de la physique classique.
Alors que le photon conférait à la lumière – l’onde lumineuse – un caractère corpusculaire, Louis de Broglie appliqua l’idée inverse aux particules matérielles. Il émit l’hypothèse que le comportement des particules (les particules connues à l’époque étaient l’électron, le proton et le neutron) pouvait à son tour être décrit à la fois comme la manifestation d’un corpuscule et la manifestation d’une onde. Il associa donc une onde à chaque particule matérielle et développa une mécanique pour manipuler ces nouveaux êtres : la mécanique ondulatoire.
Selon la mécanique ondulatoire, à toute particule est associée une onde dont la longueur d’onde est inversement proportionnelle à l’énergie de la particule. Il s’ensuit que plus une particule est énergétique (plus sa vitesse est grande), plus la longueur d’onde qui lui est associée est courte.
L’idée de Louis de Broglie sera expérimentalement vérifiée par les physiciens américains Clinton Joseph Davisson, Lester Halbert Germer et le britannique George Paget Thomson. Ils montrèrent qu’un faisceau d’électrons dispersés par un cristal génère une diffraction caractéristique d’une onde.
La notion ondulatoire de la particule permet au physicien australien Erwin Schrödinger de développer une équation dite équation d’onde pour décrire les propriétés ondulatoires de la particule et, plus particulièrement, le comportement de l’électron dans l’atome d’hydrogène.
Quoique cette équation différentielle soit continue et ait des solutions en tous les points de l’espace, les solutions admissibles sont limitées par certaines conditions exprimées par les équations mathématiques, appelées équations caractéristiques. L’équation d’onde de Schrödinger présente donc quelques solutions discrètes seulement, ces solutions sont des expressions
mathématiques dont les paramètres représentent les nombres quantiques. (Les nombres quantiques sont des entiers introduits dans la physique des particules pour exprimer la grandeur de certaines quantités caractéristiques des particules ou des systèmes.) L’équation de Schrödinger est résolue pour l’atome d’hydrogène et amène à des conclusions en accord substantiel avec la théorie quantique précédente. De plus, elle apporte une solution pour l’atome d’hélium, problème que la première théorie n’avait pas pu expliquer de façon adéquate, et demeure ici aussi en parfait accord avec les mesures expérimentales. Les solutions de l’équation de Schrödinger indiquent aussi que les quatre nombres quantiques de deux électrons ne peuvent pas être les mêmes (deux électrons ne peuvent pas occuper le même état énergétique). Cette règle, déjà établie empiriquement par le physicien suisse Wolfgang Pauli, en 1925, est appelée principe d’exclusion.
Mécanique matricielle
Parallèlement au développement de la mécanique ondulatoire, Heisenberg développe une nouvelle méthode d’analyse mathématique connue sous le nom de mécanique matricielle. D’après la théorie d’Heisenberg développée en collaboration avec les physiciens allemands Max Born et Ernst Pascual Jordan, cette formule n’est pas une équation différentielle mais plutôt une matrice: une zone qui consiste en un nombre infini de lignes dont chacune est constituée d’un nombre infini de grandeurs. La mécanique matricielle introduit la notion de matrices infinies pour représenter la position et le moment d’un électron à l’intérieur d’un atome. Il existe différentes matrices, pour chacune des autres propriétés physiques observables associées au mouvement d’un électron, comme l’énergie et le moment cinétique. Tout comme les équations différentielles de Schrödinger, ces équations matricielles sont solubles; en d’autres termes, il a été possible de les manipuler pour obtenir les
résultats prédits, comme par exemple les différentes fréquences des raies dans le spectre d’hydrogène et les autres grandeurs observables. À l’instar de la mécanique ondulatoire, la mécanique matricielle est en accord avec la première théorie quantique dans tous les processus pour lesquels cette dernière confirme les observations expérimentales; elle est même utile pour expliquer les phénomènes que la première théorie quantique ne pouvait interpréter.
Par la suite, Schrödinger réussit à prouver que les mécaniques ondulatoire et matricielle sont deux versions mathématiques différentes de la même théorie, aujourd’hui appelée mécanique quantique. Même pour le simple atome d’hydrogène constitué de deux particules, les deux types d’interprétation mathématique sont extrêmement complexes. Le prochain atome le plus simple, celui d’hélium, possède trois particules; pourtant, ce problème de trois corps (qui consiste à décrire les interactions
mutuelles des trois corps séparés) n’est pas encore complètement résolu, même pas dans la dynamique classique dont l’expression mathématique est relativement simple. Il est cependant possible de calculer les niveaux d’énergie. Pour l’application de la mathématique de la mécanique quantique à des situations relativement complexes, le physicien peut utiliser l’une des nombreuses formulations. Ce choix sera déterminé par celle qui conviendra le mieux afin d’obtenir une solution approximative convenable. Bien que la mécanique quantique décrive les phénomènes observés en termes purement mathématiques, il est possible de donner une description grossière de ce que l’atome est censé être aujourd’hui. Une série d’ondes stationnaires entourent le noyau; ces ondes ont des sommets en certains points; chaque onde stationnaire complète représente une orbite. La valeur absolue du carré de l’amplitude de l’onde en un point de l’espace à un moment donné est la probabilité d’y trouver l’électron.
Ainsi apparaît désormais l’impossibilité de prédire la présence d’un électron en un point précis à un moment donné (principe d’incertitude).
Le principe d’incertitude
L’impossibilité de localiser un électron avec exactitude à un moment précis est analysée par Werner Heisenberg qui, en 1927, formule le principe d’incertitude.
Ce principe stipule l’impossibilité de déterminer simultanément la position exacte et le moment d’une particule.
En premier lieu, il est impossible de mesurer la position d’une particule sans perturber sa vitesse.
Les connaissances de la position et de la vitesse sont dites complémentaires, c’est-à-dire qu’elles ne peuvent pas être précisées simultanément.
Ce principe est aussi fondamental si l’on veut comprendre la mécanique quantique telle qu’elle est conçue aujourd’hui: les caractères ondulatoire et corpusculaire du rayonnement électromagnétique peuvent être compris comme deux
propriétés complémentaires du rayonnement.
Depuis 1925, aucun déficit essentiel n’a été découvert dans la mécanique quantique; pourtant la question de savoir si cette théorie doit être considérée comme complète a été soulevée. Dans les années 1930, l’application de la mécanique quantique et d’une relativité spéciale sur la théorie de l’électron permettent au physicien britannique Paul Dirac de formuler une équation qui sous-entend l’existence du spin de l’électron. Par la suite, cette équation conduira à la découverte de l’existence du positron par le physicien américain Carl David Anderson.
L’application de la mécanique quantique au domaine du rayonnement électromagnétique permet d’expliquer beaucoup de phénomènes tels que le rayonnement de freinage (rayonnement émis par les électrons freinés dans la matière) et la formation de paires (formation d’un positron et d’un électron suite à l’interaction entre l’énergie électromagnétique et la matière). Néanmoins, elle soulève un problème grave appelé difficulté de divergence: certains paramètres, comme la masse simple et la charge simple de l’électron, semblent être infiniment grands dans les équations de Dirac. (Les expressions masse simple et charge simple se réfèrent à des électrons hypothétiques n’ayant d’interaction avec aucune matière et aucun rayonnement; en réalité, les électrons ont toujours une interaction, ne serait-ce qu’avec leur propre champ électrique.) Ce problème est résolu partiellement en 1947-1949 dans le cadre d’un programme nommé renormalisation, développé par le physicien japonais Shin’ichiro Tomonaga, les physiciens américains Julian S.Schwinger et Richard Feynman et le physicien américain d’origine britannique Freeman Dyson. Dans ce programme, la masse et la charge simples de l’électron sont infiniment grandes, de sorte que les autres grandeurs physiques infinies de l’équation sont négligeables. La renormalisation a permis d’augmenter considérablement la précision avec laquelle la structure de l’atome peut être analysée.
Nouvelles recherches
La mécanique quantique sert de base aux tentatives actuelles visant à expliquer la force nucléaire et à développer une théorie unifiée pour toutes les interactions fondamentales de la matière. Toutefois, il existe encore des doutes sur l’intégralité de la théorie quantique. La difficulté de divergence, par exemple, n’est que partiellement résolue. Au moment où la mécanique de Newton est rectifiée par la quantique et la relativité, plusieurs scientifiques (dont Einstein) prédirent de profonds changements dans la mécanique quantique. De grosses difficultés d’ordre théorique persistent par exemple entre la mécanique quantique et la théorie du chaos, qui connut un essor rapide dès les années 1980. Des efforts visant à développer un système capable de concilier la relativité et la mécanique quantique sont actuellement déployés par des théoriciens tels que le physicien britannique Stephen Hawking
Succès n’est peut-être pas vérité , mais on doit néanmoins noter que la mécanique quantique est la théorie physique qui a battu tous les records de réussite.
On lui doit les transistors et l’existence concrète des ordinateurs.
Pourtant quoique Einstein ait donc contribué à la naissance même de la mécanique quantique, il la détestait.
Se pourrait-il que Einstein ait eu tord et que
« Dieu joue aux dés » !
Et, si c’est l’incertain dès le départ !
L’incertain comme fondement, alors.
C’est cette idée folle qui germa chez Chaïtin.
Il se peut que le problème soit plus vaste et que Gödel et Turing sont juste le dessus de l’iceberg.
Il se peut que les choses soient pires et que ce que nous avons réellement là, en mathématique pure, ce soit l’aléatoire.
En d’autres mots , il se peut que parfois la raison pour laquelle on ne puisse pas prouver une chose, ce n’est pas parce qu’on est stupide ou que l’on ait pas assez travaillé assez longtemps dessus, il se peut donc que cette raison de ne pas trouver de preuves soit tout bonnement qu’il n’y a rien derrière !
Parfois la raison pour laquelle on ne peut pas trouver la solution à un problème n’est pas dûe au fait qu’on ne soit pas assez sympathique ou qu’on ne soit pas assez déterminé, c’est tout simplement parce qu’il n y a pas de solution ; soit que la question mathématique n’ait pas de structure soit que la réponse n’ait pas modèle soit qu’il n’y ait ni ordre ni structure disponibles dans le monde des mathématiques pures pour essayer faire naître la compréhension.
Donc, il se peut que, parfois, la raison pour laquelle on ne voit ni modèle ni structure c’est peut-être parce qu’il n’y a justement ni modèle ni structure !
De l’aléatoire dans les entiers ?
Une des illustrations que l’on peut en avoir est de regarder comment se distribuent les nombres premiers. Il semble qu’il y ait une certaine part d’aléatoire dans la distributions des entiers premiers. C’est un des chemins que certains n’hésitent pas à prendre pour essayer d’appréhender les entiers premiers. Et cette approche stochastique se fait en plein dans la théorie des nombres qui est, disons-le tout net, le cœur même des mathématiques pures.
D’un côté on n’hésite plus à user de probabilités pour tenter de comprendre les entiers premiers. Ce qui est une approche plutôt heuristique et peut-être même cognitive.
De l’autre côté on a « Dieu qui joue aux dés en physique fondamentale » ce qui exprime l’idée que ce qui se passe au niveau le plus bas de la matière est de nature aléatoire.
Comment, alors ne pas commencer à soupçonner que, peut-être, il en va de même dans les fondations même des mathématiques.
C’est en tous cas ce qu’a pensé Chaïtin.
Une première étape était de clarifier la notion d’aléatoire.
Mais qu’est-donc l’aléatoire ?
Qu’est-ce qu’on entend par absence de structure, absence d’ordre, absence de modèle ?
Aléatoire : absence de structure
C’est plus une sorte de notion de nature logique de l’aléatoire qu’une notion de nature statistique.
Ce n’est pas comme en physique où on peut dire qu’un processus est aléatoire comme le jet d’une pièce de monnaie. On ne se préoccupe pas d’où viennent les objets.
On examine quelque chose et on dit si cette chose possède une structure ou un modèle ou non.
Donc ceci est de nature logique ou structurellement aléatoire et s’oppose à la non-prédicabilité et l’aléatoire physique.
C’est différent.
C’est très lié, mais c’est différent.
Et l’idée qui vint avec – et Kolmogorov eut de façon indépendante en même temps la même idée– c’est l’idée que quelque chose est aléatoire quand on ne peut pas substituer à sa description, une autre description strictement plus petite. On parlera plutôt de compression au lieu de substitution et de concision au lieu de petitesse.
En d’autres mots une théorie n’est pas compressible lorsqu’il n’existe pas d’autre théorie plus concise qui la reproduise.
Par exemple, un ensemble de données physiques serait aléatoire si la seule façon d’exhiber l’ensemble de données était sous la forme d’une table, mais s’il existe une théorie, on peut compresser un grand nombre d’observations en un nombre petit de lois ou de principes physiques.
Et plus la compression est grande et meilleure est la théorie : en accord avec le principe d’Occam, la meilleure des théories est la plus simple des théories.
On peut soutenir, qu’en fait, un programme n’est rien d’autre qu’une théorie.
Si on se représente une théorie comme un programme qui calcule des observations. Plus le programme est petit, par rapport à la sortie qui constitue l’ensemble des observations, et meilleure est la théorie que représente ce programme.
C’est aussi ce que font les axiomes. Il y a là, la même idée dans les axiomes.
On a un grand nombre de théorèmes ou de vérités mathématiques et on arrive à les compresser sous la forme d’un système d’axiomes.
L’intérêt de cela est en fait l’économie du risque.
N’oublions pas que les axiomes sont des hypothèses qu’on doit faire et à chaque fois .
A chaque fois, qu’on fait une hypothèse on doit croire à cela et il s’introduit une part de risque.
On ne peut pas prouver à partir de rien du tout, on doit donc prendre l’axiome comme donnée. Dans un raisonnement, moins on introduit de supposition et plus sain il sera.
Donc moins on a d’axiomes et mieux c’est.
Donc, plus on aura de théorèmes compressés en un corps de théorie, et le mieux ce sera, et ceci aussi bien en mathématique qu’en physique.
On doit définir en premier la notion de manque de structure ou d’aléatoire. Si on trouve de l’aléatoire ou un manque de structure ou un manque de modèle en mathématiques pures, on doit d’abord dire ce que l’on entend par là.
Théorie algorithmique de l’information
Chaïtin appelle cela la théorie algorithmique de l’information. Cela concerne l’information algorithmique. On peut aussi dire complexité ou complexité en-taille-de-programme.
Algorithmique Information
Le concept de base est de regarder la taille du programme le plus concis, le plus petit programme
– on ne se préoccupe pas du temps d’exécution-
– c’est le programme le plus concis qui calcule un objet. C’est le nombre de bits qu’on doit à un programme pour qu’il soit capable de produire cet objet. C’est la description algorithmique la plus concise d’un objet et c’est ainsi qu’on mesure sa complexité, le contenu de son information algorithmique ou sa complexité en terme de taille de programme.
C’est comme la théorie récursive des fonctions : on ne se préoccupe pas du temps d’exécution.
Alors que se passe-t-il donc quand on commence à regarder la taille des programmes ?
Un objet est aléatoire si le plus petit programme qui le calcule a la même taille que lui et il n’y a aucune compression possible.
Donc l’idée globale c’est de regarder la taille des programmes d’ordinateur, en ne tenant pas compte du temps d’exécution, même si ça demande un milliard d’année, l’information est la seule chose qui compte, le nombre de bits d’information, la taille des programmes.
Que se passe quand on commence à jouer avec cette idée ?
Ce qui se passe, en fait, c’est que partout où on se tourne on obtient l’incomplétude et l’indécidabilité, et on l’obtient de pire des manière possibles.
Par exemple, ceci arrive avec la première des choses qu’on veut faire : on ne peut jamais décider si une chaîne individuelle de digits satisfait cette définition de l’aléatoire.
Impossible ! On ne peut jamais calculer complexité en-taille-de-programme de quoi que ce soit.
On ne peut jamais déterminer quelle est la taille du plus petit programme.
Si on a un programme qui calcule quelque chose, qui donne une borne supérieure, sa taille est une borne supérieure de la complexité en taille de programme de ce qu’il calcule. Mais on ne peut jamais prouver aucune borne inférieure.
Et c’est le premier résultat d’incomplétude de Chaïtin.
En théorie normale de la complexité celle où on tient plus compte du temps que des bits d’information, les bornes inférieures sont beaucoup plus difficile que les bornes supérieures. Obtenir une borne inférieure est beaucoup plus difficile que d’obtenir une borne supérieure. Parce quand on trouve un algorithme plus astucieux on a en même temps une borne supérieure du temps qu’il faut pour calculer quelque chose ; si on trouve une méthode qui soit rapide on a, en fait, montré en même temps aussi que cela peut se faire avec cette rapidité.
Le vrai problème est de montrer que l’on a l’algorithme le plus rapide possible.
Ce qui est plus difficile.
Mais cela peut être fait dans certain cas, pour une classe d’algorithmes possibles.
Maintenant, en Information Algorithmique (on ne tient plus compte du temps) ce n’est plus du tout possible et on peut prouver aucune borne inférieure.
L’idée de base est qu’on ne peut prouver aucune borne inférieure en terme de complexité en-taille-de-programme d’objets individuels. Donc en particulier même si la plupart des chaînes de digits satisfont à cette définition de l’aléatoire, ils sont incompressible dans ce sens, ils sont aléatoires dans le sens de l’absence de structure caractéristique.
On peut s’apercevoir très facilement que la plupart des objets qui satisfont cette définition n’ont pas de structure. Si on regarde toutes ces centaines de nombres digitaux, presque tous n’ont pas de structure selon cette définition, mais on ne peut jamais en être sûr dans des cas individuels.
On ne peut pas prouver l’absence de structure dans les cas individuels .
Plus précisément, il peut y avoir finitairement plusieurs exceptions.
Avec N bits d’axiome on peut déterminer tous les objets dont la complexité en taille de programme est au plus N. Mais c’est le plus loin où on peut aller.
Un nombre encore plus complexe que le plus complexe des nombres transcendants connus: Omega
Le pire résultat de Chaïtin sur l’incomplétude quand on a affaire à une absence totale de structure en mathématiques pures nécessite l’introduction d’un nombre qu’il appelle la probabilité d’arrêt.
Ω = probabilité d’arrêt
Considérons le réel Ω qui est la probabilité qu’un programme tiré au hasard s’arrête. C’est une moyennisation du problème de l’arrêt d’une machine de Turing. Et ,pourvu que le langage de programmation soit spécifié ceci donne un nombre réel bien déterminé.
Ωmachine = probabilité d’arrêt.
Donc dés qu’on le décide Ω est un nombre réel et bien défini. Mathématiquement, ce n’est pas un objet très sophistiqué. Cependant il ressort de cet objet Ωqu’il est maximalement inconnaissable !
Ω est maximalement inconnaissable
Que veut dire exactement l’expression maximalement inconnaissable.
Cela concerne les bits ou les digits de ce nombre.
Une fois fixé le langage de programmation de la machine cette probabilité d’arrêt , nous l’avons dit, est un nombre réel bien spécifique, qui dépend du choix de la machine ou du langage de programmation dans lequel on génère au hasard un programme.
Ce nombre spécifique, écrivons-le en binaire, et donc on obtient une séquence de 0 te de 1.
Il s’avère que ces 0 et ces 1 ne font apparaître aucune structure.
Ils ne peuvent pas être compressés.
Pour calculer les N premiers bits de ce nombre binaire cela exige un programme de N bits.
Pour prouver ce que sont ces N premiers bits de ce nombre ceci exige N bits d’axiomes.
C’est une information mathématique irréductible.
Une information mathématique irréductible ?
Voilà une idée qui ne manque pas d’être absolument choquante parce qu’une idée normale en mathématique, une de ces bonnes idées à la Hilbert, doit être telle que toute vérité mathématique peut être réduite à un petit ensemble d’axiomes qu’on peut accepter et qui seraient, si possible, self-évidents.
Mais si on veut déterminer quels sont les bits de la probabilité d’arrêt , ceci ne peut pas être réduit par quelque chose d’autre qui soit plus simple.
Ω possède une définition mathématique avec une structure plutôt simple dès qu’on spécifie l’ordinateur ou le langage de programmation et Chaïtin a même écrit un programme en LISP qui calcule ce nombre au sens faible.
Bien que Ω soit maximalement inconnaissable on peut toujours essayer de l’obtenir comme limite à partir la formule ci-dessous
Ω= ∑ p s’arrête 2 –|p|
Mais cela converge très, très très, très, lentement –on ne peut jamais savoir de combien on est proche du nombre à calculer
—il n’existe pas de régulateur calculable de la convergence et il n’y a pas moyen de décider de ce qu’il reste à faire pour obtenir les N premiers bits de Ω.
Pour obtenir Ω à la limite à partir de la formule ci-dessous, on doit considérer de plus en plus de programmes de plus en plus longtemps et à chaque fois qu’on voit un programme s’arrêter, ceci contribue de 1/2k à la probabilité d’arrêt.
Ω= ∑ p s’arrête 2 –|p|
Donc le temps qu’il faut pour obtenir les N premiers bits de Ω croît comme le temps d’exécution fini, le plus long, d’un programme de N bit.
De manière plus précise on peut dire que chaque programme qui permet de définir Ω doit être généré aléatoirement comme par le jet d’une pièce de monnaie pour chacun de ses bits. Le point crucial est que le programme doit être auto-délimité. L’ordinateur doit obtenir le programme bit après bit. Chaque fois que l’ordinateur demande un bit du programme, on jette la pièce à pile ou face. Et l’ordinateur doit décider de lui-même s’il a suffisamment de bits c’est à dire s’il a le programme entier. Le programme doit être auto-délimité pour définir cette mesure de probabilité correctement. Il n’y a pas de blanc pour indiquer la fin d’un programme : un programme doit indiquer en lui-même l’information de sa propre longueur à l’aide d’une certaine astuce, d’une certaine astuce codée. C’est le seul aspect technique pour obtenir que cette probabilité soit bien définie.
C’est aussi le point technique de la théorie de Chaïtin.
Ω est donc un nombre compris entre 0 et 1. C’est la probabilité qu’un programme dont les bits ont été générés aléatoirement par les jets indépendants d’une pièce de monnaie non-faussée, s’arrête.
Pour fixer les idées, le langage de programmation choisi par Chaïtin est LISP et la machine est une machine de Turing.
Donc Ω est maximalement inconnaissable. C’est un cas où la vérité mathématique n’a ni structure ni modèle et c’est quelque chose que nous n’aurons jamais.
Ce qui a été obtenu là est de l’aléatoire au maximum.
n C’est analogue aux jets indépendants d’une pièce de monnaie en mathématiques pures.
Ω En fait, Chaïtin peut aussi le faire, à la manière de Gödel, dans la théorie élémentaire des nombres. Chaïtin a construit la détermination des bits de à partir d’une équation diophantienne.
Équations diophantienne indécidabilité et omega
De nombreux travaux ont été effectués à partir de la preuve de Gödel, et ceux-ci ont montré que les problèmes ayant trait à la calculabilité sont équivalents aux problèmes arithmétiques sur les nombres entiers. Plusieurs noms viennent à l’esprit. Julia Robinson, Hilary Putnam et Martin Davis ont réalisés des travaux parmi les plus importants et le résultat fondamental a été trouvé en 1970 par Youri Matyassevitch. Il a construit une équation diophantienne, c’est-à-dire une équation algébrique qui met en œuvre uniquement des nombres entiers et un certain nombre de variables. Une de ces variables, appelons-la K, joue le rôle d’un paramètre. C’est une équation polynomiale avec des coefficients entiers et toutes les inconnues doivent également être des nombres entiers ; voilà la définition d’une équation diophantienne. Comme déjà dit, l’une de ces inconnues est un paramètre, et l’équation de Matyassevitch possède une solution pour une valeur particulière du paramètre K si et seulement si le Kième programme d’ordinateur s’arrête. Matyassevitch a montré en 1970 que ce problème est équivalent à celui de décider si un programme quelconque s’arrête. Le halting problem de Turing est donc exactement aussi difficile que le dixième problème de Hilbert. Il est rigoureusement aussi difficile de décider si un programme quelconque s’arrêtera que de décider si une équation diophantienne quelconque possède une solution. Il n’existe par conséquent aucun algorithme qui permette de réaliser cela, et ainsi, le dixième problème de Hilbert ne peut pas être résolu; tel est le résultat obtenu par Matyassevitch en 1970
Chaïtin est parvenu à une équation diophantienne exponentielle possédant un paramètre. L’expression « équation diophantienne exponentielle » signifie simplement que les variables peuvent être des exposants. C’est une différence avec Matyassevitch qui a montré que le dixième problème de Hilbert n’est pas résoluble en se servant d’équations diophantiennes polynomiales, ce qui signifie que les exposants y sont toujours des nombres entiers naturels constants. Chaïtin autorise quant à lui des expressions telles que XY. On ne sait pas encore si cela est véritablement nécessaire. Il se pourrait que l’on puisse arriver à un résultat similaire avec une équation diophantienne polynomiale. C’est une question ouverte, ‘elle n’a pas encore été réglée. Pour l’instant, il a obtenu une équation diophantienne exponentielle possédant dix-sept mille variables. Cette équation tient sur deux cent pages et une des variables est un paramètre.
Il s’agit d’une équation où chaque constante est un nombre entier naturel et où toutes les variables sont également des nombres naturels positifs (autrement dit, ce sont des entiers non-négatifs). L’une de ces variables est donc un paramètre, et l’on peut modifier la valeur de ce paramètre qui peut être égal à 1, 2, 3, 4, 5, etc. On se demande alors si cette équation possède un nombre fini ou infini de solutions. L’équation est construite de telle manière qu’elle a un nombre fini de solutions si un bit particulier de Oméga vaut 0, et elle a un nombre infini de solutions si ce bit est égal à 1. Décider si, pour chacun des cas particuliers, cette équation diophantienne exponentielle possède un nombre fini ou infini de solutions est donc exactement identique à la détermination d’un bit spécifique de la probabilité d’arrêt :
0 < Ω= ∑ p s’arrête 2 –|p| < 1
Chaïtin a construit cette équation de deux cent pages de telle façon qu’elle possède un nombre fini ou un nombre infini de solutions en fonction de la valeur 0 ou 1 d’un certain bit de la probabilité d’arrêt Oméga. Lorsque l’on varie le paramètre de cette équation, on obtient chacun des bits de Oméga. L’équation de Matyassevitch est construite de telle sorte qu’elle possède une solution si et seulement si un programme particulier s’arrête. Et lorsque l’on varie le paramètre de l’équation de Matyassevitch, on obtient tous les programmes d’ordinateurs.
L’équation de Matyassevitch fournit N questions arithmétiques qui possèdent une réponse de type oui/non et produit seulement log N bits d’information algorithmique. L’équation de Chaïtin conduit à N questions arithmétiques qui possèdent également une réponse de type oui/non ; elle génère par contre une information mathématique irréductible et incompressible
Comment ? De l’incomplétude partout !
Ici nous sommes face à une question mathématique simple: quelle est la valeur de chaque bit de Ω ? Est-ce que le premier bit est 0 ou 1, est-ce que le second bit est 0 ou 1 est-ce que le troisième bit est 0 ou 1… Mais les réponses n’ont pas de structures et ressemblent aux jets indépendants d’une pièce de monnaie non-faussée, bien que chaque réponse soit bien définie mathématiquement, parce que c’est le bit spécifique d’un nombre réel spécifique
En fait nous n’en saurons jamais rien : ici nous n’avons que la version des jets indépendants d’une pièce de monnaie de Chaïtin.
Même si on connaissait tous les bits de rangs pairs de Ω cela n’aiderait le moindre du monde à déterminer les bits de rangs impairs.
Et si on connaissait le premier million de bits de Ω,ce million d’informations supplémentaires ne permettrai pas plus d’obtenir la valeur du bit suivant.
Cela ressemble vraiment aux jets indépendants d’une pièce de monnaie, c’est maximalement aléatoire et ça a une entropie maximale.
Les physiciens sont souvent à l’aise avec l’aléatoire mais il revient en fait au noir ou blanc des mathématiques pures de Hilbert.
Ici nous avons autre chose.
Chaque bit est très précisément défini.
C’est soit 1 soit 0 .
Parce Ω est un nombre réel spécifique dès que l’on a fixé la machine ou le langage de programmation.
La situation est si rigoureusement équilibrée entre la valeur 1 et la valeur 0 qu’il ne faut plus penser en terme de blanc ou noir pour chaque bit.
Traditionnellement si quelque chose est vraie c’est à cause d’une certaine raison, en mathématique quelque chose de vraie est appelé une preuve et le travail des mathématiciens est de rechercher les preuves et donc de rechercher les raisons qui font que quelque chose est vraie.
Mais les bits de Ω que ce soit 0 soit 1 sont des vérités mathématiques qui sont vraies sans raison
Elles sont vraies par comme accident !
En d’autres mots, ce n’est pas seulement que Hilbert ait été légèrement dans l’erreur. Ce n’est pas que quelque chose soit légèrement faux et qu’il y ait quelques trous dans les idées mathématiques normales et qui sont des cas dégénérés comme « cette proposition est non-démontrable.
Ce n’est pas cela .
C’est pire !
Il y a des cas extrêmes où des vérités mathématiques n’ont pas de structures du tout où nous sommes face à l’inconnaissance maximale.
On a des vérités mathématiques juxtaposées, indépendantes à la manière dont les jets d’une pièce de monnaie peuvent être indépendants.
Une série d’assertions dont les vérités sont sans liens possibles.
Des vérités sans causes.
Comme par accident.
Résumons tout cela
Avec Gödel l’incomplétude est une surprise, il n’existe pas d’ensemble fini d’axiomes pouvant contenir toute la vérité mathématique.
Avec Turing , l’incomplétude apparaît plus naturelle.
Avec Chaïtin, en considérant la taille des programmes, l’incomplétude est inévitable.
Voyons comment reformuler donc que la découverte de Gödel est somme toute normale et naturelle.
Physique et indécidabilité
On sait que Newton Da Costa et Francisco Doria [« Undecidability and Incompletness in Classical Mechanics » . International Journal of Theoretical Physics, 30 (1991)] ont été capable de prouver l’existence de l’indécidabilité dans des théories physiques comme la théorie classique de l’électromagnétisme, la théorie du chaos, la physique quantique et les théorie de dite de jauge et mêm la théorie au bon comportement qu’est la mécanique classique .Leur preuve a été établie à partir d’un résultat de Richardson, qui a montré l’existence de propositions indécidables sur les fonctions à valeurs réelles, résultat qui provient d’ailleurs du célèbre théorème de Davis, Matijasevic, Robinson qui établit l’indécidabilité de l’équation de Diophante à coefficient entiers que nous avons déjà cité dans le cadre des travaux de Chaïtin.
Sont classées comme indécidables par Newton Da Costa et Francisco Doria les questions suivantes :
- Est-ce qu’il existe un algorithme général pour décider si un Hamiltonien donné représente une particule singulière libre ou un oscillateur harmonique ?
- Étant donné un Hamiltonien h, est-ce qu’il existe un algorithme capable de nous dire si l’Hamiltonien Ha du système dynamique associé est intégrable ou pas ?
- Étant donné un Hamiltonien h tel que Ha puisse être intégré par des quadratiques, peut-on trouver une transformation canonique adéquate pour cette intégration ?
- Peut-on vérifier algorithmiquement si un ensemble arbitraire de fonctions est un ensemble d’intégrales premières pour un système Hamiltonien.
Newton Da Costa et Francisco Doria ont construit une correspondance comme une sorte pont entre une algèbre de fonctions réelles bien définies et les polynômes qu’ils ont d’ailleurs appelé « Foncteur de Richardson » et qui a permis de la translation des propriétés d’indécidabilité des équations de Diophante dans le langage des fonctions élémentaires qui coïncide avec l’analyse réelle classique.
Une expression correspondant au problème de l’arrêt de Turing peut alors être explicitement et algorithmiquement construite en n’utilisant exclusivement que des élément de l’analyse c’est à dire des fonctions élémentaires, des intégrales, des dérivées.
D’autres chercheurs [Karl Svozil, Calude …]arrivent aux mêmes conclusions d’indécidabilité en utilisant une transduction des phénomènes de la physique par le calcul (l’expérience physique est vue à travers une certaine équivalence avec une simulation en machine.)
C’est un constat via le calcul et cela nous semble reposer plutôt sur une position de principe mécaniste que Bruno Marchal a su dans thèse[] analyser par rapport à la position cognititiviste
Physique mesure et problème
Une première façon serait de faire appel à l’idée physique qu’on se fait de l’aléatoire où l’aléatoire se trouve associé à ce qui n’est pas significatif (en se rappelant que ce qui est significatif en physique est ce qui a trait à la mesure – que cette mesure soit directe ( sans relais de déduction) ou indirecte (avec relais de déduction)
Dans le processus de mesure directe, l’expérimentation sur le réel est ramenée à des protocoles rigoureux où certains paramètres sont contrôlés et astreints à un invariance complète si cela est possible ou à une invariance relative et il existe une relationnelle généralement simple liant les paramètres de contrôle à partir de laquelle on peut déduire complètement les valeurs globales et séparées de chacun des paramètres liés à partir d’une valeur locale de ces paramètres qui correspond à un choix unique du point temporel où se fera la mesure des valeurs de départ de ces paramètres liés.
Idéalement, il est supposé possible d’associer au réel un espace abstrait non nécessairement constructible (i.e. simulable par des processus finis et des ressources finies) capable d’instancier des images cohérentes du réel. A paramètres fermés et contrôlés, cette instanciaton porte généralement sur la prévision du comportement du ou des paramètres laissés libres dans l’espace de modélisation. L’inconnu peut porter sur l’espace lui même, ses dimensions, sa topologie, la possibilité ou non- d’admettre des sous-espaces ou des fermetures de sous-espaces dotés de propriétés d’invariance locales et/ou globales susceptible de formaliser des prédictions globales vraies à partir d’informations locales observées.
C’est le cas quand, par exemple où à partir de l’observation des caractéristiques attachées à un seul point matériel à un instant donné (conditions initiales) on se donne une théorie pour pouvoir décrire de proche en proche toute sa trajectoire à l’avance que l’on puisse valider par la confrontation avec les observations et mesures que l’on peut faire en n’importe quel instant ultérieur au point de départ (qui lui coïncide par définition) de la trajectoire réelle du point matériel.
Il faut aussi signaler que pour les physiciens l’univers reste égal à lui même (il n’y a pas de surgissement de matière supplémentaire du néant) d’où il découle des principes de conservation de base que tout bon modèle doit être capable de rendre.
Par analogie avec l’automatique, on peut parler d’état initial pour désigner l’observation ou la donnée des conditions initiales, atteindre un état final spécifié à l’avance définie une trajectoire qui avait été prévue. On peut dire que le problème en physique est essentiellement la détection de phénomènes physiques dont une information locale est généralement possible à obtenir et dont des comportements de type globaux ne sont déductibles d’aucun des modèles connus de la physique actuelle.
L’impossibilité, même au plan conceptuel, de contrôle du comportement de ces phénomènes en découle.
Avec ce critère, on voit que la physique connaît d’innombrables incomplétudes.
Citons les irruptions volcaniques et les phénomènes météorologiques impressionnants mais aussi plus modestement par exemple la trajectoire d’une goutte d’eau dans l’atmosphère. La prévision dans ces domaines s’appuie sur des inférences de type stochastique et dont les résultats restent bien entendu de type stochastiques.
Les présupposés de la démarche en physique et la mesure
Alors que dans le processus de mesure directe la prévision est directement déduite d’un modèle d’observation et d’un modèle de déduction couplés représentables en même temps directement (il est possible de concevoir des protocoles d’expérimentation à l’avance où on isole l’évolution d’un paramètre et ce sont bien des valeurs qui seront recueillies en tant que résultats de l’expérimentation et qui seront confrontées aux valeurs prévues), dans les mesures indirectes la mesure découle à la fois de l’évolution d’un ou de plusieurs paramètres et utilise des formules supposées vérifiées par ces paramètres. C’est une expérimentation contenant en imbrication une des expérimentations virtuelles dont les sorties sont des dépendances fonctionnelles des entrées; c’est une expérimentation qui capitalise l’acquis et est donc plus complexe dans la mesure où elle contient virtuellement des prédictions potentielles supposées valides. Le champ des inconnues englobe alors les lois physiques elles-mêmes introduisant une récursivité cruciale dans la démarche de la physique.
Le couple binaire traditionnel de la démarche, Problèmes, Solutions avec les sous-phases respectives d’éclatements des problèmes en sous-problèmes et de recompositions de solutions en solutions s’enrichit d’un élément ternaire médian ayant les caractéristiques à la fois des solutions et des problèmes et que l’on peut dénommer Solution-inverse et qui signifie en raccourcis :quel est le (ou la classe de ) problème qui correspond aux solutions (construites ou reconstruites)que j’observe.
La démarche traditionnelle guidant l’inférence en physique passe de l’oscillation binaire entre le connu et l’inconnu à un cycle ternaire intégrant un nouvel état hypothétique entre le connu et l’inconnu.
Il correspond alors des protocoles d’expérimentations plus complexe à réaliser dans la mesure où c’est la loi elle-même qui peut-être une variable dont il faut au préalable identifier les paramètres et le type de liaison fonctionnelle. Il y a interaction entre le modèle et les liaisons supposées entre les paramètres . La validation maximale étant requise, des techniques de filtrage utilisant les mesures expérimentales et le modèle sont nécessaire pour la construction effective d’une solution.
Cette imbrication exige alors une pertinence à-priori de la mesure.
Stabilité et pertinence de l’indicateur de mesure
Bien sûr la valeur de mesure permet de comparer et en général de hiérarchiser, mais la principale garantie de la fiabilité de la mesure repose sur le principe de la possibilité de sa réplication à l’infini qui consiste à obtenir la même valeur à chaque fois que la même expérimentation est effectuée donc, même et y compris si on refait cette expérimentation une infinité de fois, on doit obtenir une population infinie de valeurs stables autour d’une même valeur centrale qui indiquera la mesure .
(On peut remarquer que la valeur représentant la mesure peut tout à fait être non-numérique pourvu que l’on puisse y déduire un certain ordre )
Cette population infinie de mesures idéalement est constituée donc d’un même nombre répété à l’infini. Dans la pratique cette population est représentée par une sous-population finie de mesures
Car on ne peut pas faire une même expérimentation une infinité de fois.
De plus n’importe quel élément de la sous-population est sensé représenter la mesure.
On s’attend à une constante comme élément répété à l’infini dans ce champ potentiel correspondant à la mesure d’une expérimentation idéalement répétée une infinité de fois. Des valeurs différentes dans le champ disqualifieraient la mesure qui à son tour remet en cause les conditions de l’expérimentation et peut-être même sa conception.
Ces valeurs différentes rendent donc non-représentif un élément quelconque de ce champ potentiel qui par définitif ne contient que des éléments représentatifs de la mesure de la même expérimentation.
Ne pas obtenir les mêmes résultats pour une même expérimentation, quand on la refait un nombre indéfini de foi, rend donc toute mesure faite non-significative.
Maintenant, il faut tenir compte à la fois qu’en pratique on ne peut refaire une même expérimentation une infinité de fois et que non plus on peut espérer réaliser l’égalité absolue et rigoureuse de toues ces expérimentation que l’on refait. Dans la pratique physique, Il faudra se contenter de sous-populations finies d’expérimentations et Il y aura donc des écarts entre les valeurs de mesure.
L’écart entre la plus grande valeur de la sous-population et la plus petite valeur va servir à définir une erreur de mesure qui donc idéalement pour que la mesure soit fiable au maximum doit être nulle. Car cette nullité traduit un phénomène de stabilité qui signifie qu’à chaque fois qu’une même expérimentation a été refaite la mesure obtenue a donné le même nombre. Dans la pratique, donc parce qu’on ne peut pas faire absolument et rigoureusement la même expérimentation, on s’attendra à une erreur petite. La petitesse étant une notion relative, il est bon de la ramener à l’échelle de la mesure elle-même. Autrement dit définir l’empan de crédibilité de la mesure par la mesure elle-même. Par exemple si l’erreur est de la taille de la mesure elle-même et si on l’accepte, on accepte aussi du coup 0 comme représentant de cette mesure par définition même de l‘erreur .
Ceci donc disqualifie toutes les mesures dont les erreurs et les éléments sont de même taille.
Les mesures seront dite non-significatives car les variations dans le champ sont trop importantes et sont équivalentes à des valeurs tirés au hasard sans avoir fait l’expérimentation.
Mesure et langage d’expérimentation
– donc non-significatif caractérise ce qui est hors de la mesure et non obligatoirement ce qui est faux qui lui est parfaitement significatif
Une physique qui se respecte pose donc un principe de base rationnel sérieux et postule donc que tout phénomène physique peut être mesurable.
Il faut introduire cette nuance que la mesure peut-être directe et alors les concepts opératoires correspondants sont aussi directement formulables
Mais la mesure peut aussi être indirecte et les concepts opératoires correspondants seraient dès lors indirects aussi, c’est à dire, nécessitant des relais conceptuels où plusieurs niveaux d’abstraction .
Le langage de questionnement est dans le cas direct proche d’un langage naturel où se confondent les objets et leurs représentations.
Dans le second cas, le langage de questionnement n’est plus homothétique au langage naturel de représentation des objets et nécessite un niveau différent d’abstraction des concepts de mesure.
Les concepts de ce langage nécessairement artificiel ou second n’ont alors généralement pas de systèmes de représentation naturel (i.e. la possibilité d’identifier objets et représentation de ces objets sur un même plan abstrait qui est à la base des systèmes de croyances d’où peuvent se déduire des systèmes d’explication) Autrement dit, on ne peut pas fabriquer directement des interprétations autres que formelles et qui par conséquent ne sont porteuse d’aucune sémantique .
L’ontologie des objets dans les systèmes perçus via une mesure indirecte
constitue soit une possibilité d’un ou de plusieurs objets absolument nouveaux (avec le problème, si on est en système fermé, de la création ex-nihilo) ou dualement d’une nouvelle relation primitive d’objets entre les objets primitifs des objets à mesure directe( avec le problème, si on est en système ouvert des incomplétudes emboîtées)
C’est une extension nécessaire du concept de mesure qui ne va pas bien sûr sans déclencher débat sur le mesurable et le mesuré.
-Dans le premier cas l’objet (des caractéristiques de l’objet ) est identifié par le nombre ou un faisceau de nombres Avec bien sûr, toutes les variantes possibles du schéma de mesure- l’objet est conçu à travers la représentation de ses caractères de singularité bien séparables
-Dans le second cas, une fonctionnelle plus globale (de nombres) est associée à ce qui était considérée comme une entité-objet dans le cas direct. L’objet est une entité plus globale ses caractéristiques sont plutôt des comportements et de plus, ne sont plus simplement séparables.
Le second cas indirect peut être vu comme une généralisation du cas direct avec, à cause de l’inversion du schéma de mesure, de nouveaux problèmes d’indétermination aux limites qui ne manquent pas de surgir. Mais c’est plutôt à une complexification de la mesure que nous avons à faire et les processus indirects ne se réduisent certes pas aux processus directs.
Maintenant, ce qui est non-significatif en physique constitue bel et bien le monde des objets dépourvus de sens physique, mais c’est aussi le monde potentiel des objets possibles de la physique puisque susceptibles de mesure.
C’est le monde des objets candidats à l’adhésion au club des objets de la physique.
La démarche normale de la physique est de se charger de construire un sens physique à ces objets non-significatifs.
C’est-à-dire d’associer à cet ensemble d’objets encore virtuels, une mesure qui soit significative.
Cette mesure doit naturellement rester compatible avec les mesures des objets déjà significatifs de la physique. C’est-à-dire, l’introduction de l’objet virtuel, grâce à sa toute nouvelle mesure, dans le club des objets significatifs de la physique ne doit pas remettre en cause le critère de mesurabilité des objets physiques. De faire soudain apparaître, par exemple, comme non-significatifs des objets, y compris des objets potentiels, qui sont déjà au sein du champ de la physique.
La pétition de principe en physique que tout phénomène physique est mesurable joue le rôle du tout est formalisable en mathématique avec dans le rôle du vrai, le significatif et le rôle du non-vrai, le non-significatif et dans le rôle de l’Arithmétique, l’Arithmétique.
Alors le théorème de Gödel appliqué à la physique vue comme un système formel :
Il existe au moins un phénomène physique significatif dont on ne peut avoir ni mesure significative ni de mesure non-significative.
Il y a là, d’abord, implicitement posé la décomposition-recomposition toujours possible de tout phénomène physique possible en sous-phénomènes physiques. Autrement dit une loi structurellement vraie équivalente à la récursivité est supposée s’appliquer isotropiquement dans l’Univers de la physique. La présence même implicite d’une loi est le signe qu’une catégorisation des objets en classes, est en réalité supposée possible de sorte que l’étude d’un représentant d’une classe résume les caractéristiques de tout élément de la même classe. Donc c’est la recherche de cette loi primordiale ou plutôt de ses instanciations qui sera l’objectif de la mesure.
Est donc postulé que tout phénomène physique obéit à une loi étant elle-même un objet mesurable.
La loi physique a donc clairement un statut d’objet physique mais qui ne peut pas être direct.
La loi, en physique, est donc un objet physique de statut indirect.
La loi, en physique, joue le rôle que les axiomes jouent en mathématiques.
En gros, Chaïtin montre qu’en mathématique ces objets axiomatiques lorsqu’il sont décrit dans un formalisme standard non redondant (programme minimaux de Chaïtin) – le mot clé est le qualificatif non redondant – en effet si la différentiation absolue est requise pour distinguer deux objets infiniment voisins – on voit que l’ensemble de mesure le plus économique possible est la droite des réels ( ou le segment continue [0,1] ce qui revient au même mais qui nous ramène sans étonnement aux probabilités de Kolmogorov et surtout à la mesure de Borel-Lebesgue) qui fournit une topologie compatible avec le niveau infini de précision requis des objets. Donc ces objets ont, à cause de la rigueur extrême où il sont formalisés qui exige un niveau de précision maximum, ont donc la puissance du continu .
En particulier, la probabilité attaché à un objet ponctuel quelconque du continu est nulle.
(à partir d’une Urne U continue contenant un continuum d’objets continus , on n’a aucune chance de tirer un objet continu spécifié à l’avance)
Traduisons : le choix d’un axiome particulier est de probabilité nulle (équivalente à la probabilité du choix d’un point réel sur la droite réelle)
Peut-on alors pour retourner à la question ramener les problèmes de la physique à des problèmes en Mathématiques avec des degrés de précision requis moins absolus ?
En gros, la physique n’est –elle pas ontologiquement une approximation des mathématiques ?
(et , alors pourquoi pas, inversement la mathématique n’est-elle pas une idéalisation des mathématiques ?)- on retrouve là, à une échelle différente bien sûr , peut-être tous les questionnements et les rapports dialectiques entre savoir et savoir-faire, entre la connaissance formelle et le savoir empirique-
Physiquement, et en recourant à une analogie archimédienne la situation peut se rendre de la manière suivante ; L’eau dans un seau symbolise l’aspect continu des objets continus dans l’Urne, la probabilité du côté mathématique, en tant mesure est représentée par le volume du côté de la physique (qui comme la probabilité provient en fait d’un rapport de volumes aux formes standardisés et facilement calculable comme le cube (Archimède a en fait trouvé le moyen d’exprimer un volume quelconque dans un langage opérationnalisable où la comparabilité entre deux objets barycentriques (les objets sont réduits à des ponctualités équivalentes portant une information globale de type spatiale qu’on peut identifier avec la notion physique masse inerte) qu’il est toujours possible d’extraire au besoin sous la forme de moment et qui reste représentable par le nombre) – il reste à interpréter la notion de point continu dans le continuum physique qu’est l’eau.
En effet, on peut se poser la question de la correspondance dans le milieu de l’eau de la notion de point continu et de se poser ensuite la question de la mesure de son volume.
Une manière constructible de définir un point d’eau est de le définir par le volume d’eau le plus petit possible que l’on peut déplacer par le procédé d’Archimède. L’expérience consiste à mesurer des volumes correspondant à des immersions d’objets de dimensions de plus en plus petits jusqu’à ce que cette suite décroissante de volume arrive à 0, c’est à dire que l’immersion d’un très petit objet n’a causé aucun déplacement d’eau détectable par le procédé. On peut contrôler la diminution de volumes de la suite des objets à immerger en décidant que ce seront des petits cubes dont les arêtes successives sont dans un rapport de un sur deux par exemple. En partant d’un petit cube d’un volume unité on génère la suite dégressive de petits cubes dont on connaît algébriquement par avance la suite décroissante de volumes correspondants. D’un côté nous avons des nombres représentants le volume théorique des cubes correspondants, de l’autre côté nous avons des nombres de plus en plus petits représentant la suite des volumes des objets cubiques immergés dont on a mesuré le déplacement d’eau correspondant dans le dispositif Archimédien. Alors que la suite des volumes théorique régresse sans jamais s’annuler par construction du processus de construction des petits cubes, de l’autre côté on arrive fatalement à une étape où l’immersion d’un petit objet n’entraînera aucun déplacement d’eau sensible par le dispositif et on est obligé d’arrêter le processus de mesure car à l’immersion d’un très petit cube il ne correspond physiquement, par le truchement du procédé d’Archimède, aucun déplacement d’eau.
Du fait qu’on peut contrôler le processus de construction de la suite régressive des petits objets à immerger, on en déduit que le phénomène d’absence de déplacement d’eau se produira pour une population indéfinie d’autres valeurs théoriques de volumes de petits objets immergés. Il suffit de construire ces objets en utilisant d’autre formes géométriques donnant des suites de volumes différents et /ou contrôler différemment le paramètre pilotant la régression des volumes géométriques. La plus grande de ces valeurs théoriques de petits volume ne causant pas de déplacement d’eau serait alors le volume du plus petit objet indétectable par le procédé Archimédien. Malheureusement on comprend que ce nombre risque de ne jamais être atteint puisqu’on peut concevoir une infinité de mesures successives débouchant sur un déplacement nul donnant des petits volumes toujours plus grands puisque le contrôle des suites régressives se fait géométriquement.
Dans chaque suite des petits objets à immerger à chaque fois que le phénomène de déplacement nul occure pour un petit volume d’objet on est obligé de déclarer son indétectabilité et donc c’est l’objet directement précédent dans la suite qui constitue dans la suite le plus petit objet détectable par le procédé. Pour une suite donnée, à chaque objet indétectable on peut associer un objet détectable. En considérant l’ensemble de toutes les suites qu’on peut construire et auxquelles on applique le procédé archimédien de recherche du plus petit volume d’eau, on peut déclarer qu’il y a autant d’objets détectables que d’objets non détectables.
En fait ce (plus petit) objet non détectable (dans la suite) est même la signature de l’objet détectables correspondant qui est justement déclarés plus petit objet détectable (dans la même suite) uniquement parce la mesure de l’objet qui suit a été constatée indétectable.
Maintenant, le grand Archimède nous a aussi gratifié du théorème des moments par la technique du levier sur un point d’appui ( Donnez-moi un point d’appui…)
Considérons l’ensemble de toutes les suites de mesures faites et marquons les objets successifs de chaque suite qui ont été déclaré détectable , non détectable respectivement dans chaque suite.
Pour 1 objet non détectable, mettons le dispositif d’Archimède sur le premier fléau d’un levier
Sur le second fléau du levier mettons un même second dispositif de mesure de volume d’Archimède. Il y devrait y avoir équilibre donc tant que d’un côté on immerge un objet de volume non détectable, que sur le second fléau on n’immerge aucun objet et que le point d’appui est rigoureusement au milieu géométrique des deus fléaux. Donc l’immersion dans le second fléau d’un objet déclaré détectable (le précédent dans la suite de l’objet non détectable déjà plongé dans le dispositif sur le premier fléau) doit rompre l’équilibre, le point d’appui toujours au milieu des deux fléaux.
Le théorème des moments nous garantit que si on a une distance de fléau à fléau convenable qu’on peut trouver un nouveau point d’appui en déplaçant le point d’appui vers le second fléau en déséquilibre jusqu’au rétablissement de l’équilibre. Il y a proportionnalité entre les longueurs respectives mesurant la distance des 2 dispositifs au point d’appui et les plus petits volumes correspondants respectivement au plus petit objet détecté et le plus petit objet non détecté (suivant dans la suite)
Si Vd est le volume du plus petit objet détecté par le dispositif et ld sa distance au point d’appui
Si Vx est le volume du plus petit objet non détecté par le dispositif équivalent sur le second fléau du levier et lx la distance de ce dispositif au point d’appui.
A l’équilibre des deux fléaux on a :
(Vx / Vd )=( lx / ld) et donc Vx = Vd x( lx / ld)
Ceci a été possible car nous n’avons utilisé que la notion de copie ou de duplication du dispositif archimédien à l’identique qu’on a supposé réalisable, ce qui est d’ailleurs une condition nécessaire pour la reproductibilité des expériences en physique.
La manipulation est générique et s’applique à tous les types d’indétectables que l’on a pu constater. On peut qualifier les plus petits objets non-détectable par le dispositif Archimédien (DA) comme étant des objets DA-non-détectable et détectables par application du levier au Dispositif Archimédien dupliqué de L-DA2-détectable. Nous avons alors le théorème physique :
Théorème : Tout DA-non-détectable est L-DA2-détectable.
Ceci bien entendu s’applique aux objets issus des même suites régressives, au sens du volume, d’objets.
Autrement dit on a rendu détectable ce qui était indétectable !
Soit maintenant x un objet de volume Vx et qui DA-non-détectable au sens précédent, on construit x2 de volume Vx/2 qui est à-forcériori DA-non-détectable non plus. Par le montage précédent il existe une distance lx/2 entre le dispositif où est immergé l’objet x/2et le point d’appui qui rend détectable le volume de l’objet x/2.
On réitère le processus et on a donc rendu détectables des objets de volumes de plus en plus petits : Vx ,Vx/2 ,Vx/4 ,Vx/8 ,Vx/16 ,Vx/32 ,Vx/64 … auxquels il correspond les distances respectives au point d’appui : lx ,lx/2 ,lx/4 ,lx/8 ,lx/16 ,lx/32 ,lx/64…
Comme Vx = Vd x( lx / ld)
Donc la suite des lx décroît avec la suite des volumes, comme on saurait avoir un levier de longueur infinie donc L finie est la longueur du levier (L= lx + ld ), comme Vd est un paramètre restant constant dans cette série d’expériences, il va exister une plus petite valeur lx* pour laquelle la valeur correspondante : Vx* va être L-DA2-indétectable.
Nous voilà donc tombé de Charybde en Scylla !
Nous sommes topologiquement ramenés à la situation précédente bien que l’on puisse qualifier Vx* de volume indétectable du second ordre. La sensibilité est sur les distances au point d’appui . Construisons alors le système 2-L-DA2 constitué de deux Dispositifs Archimédien dupliqués l’un dans l’état Vx* en équilibre au milieu du point d’appui l’un des fléaux contenant l’objet x* de volume indétectable Vx*, et l’autre ne contenant aucun objet immergé et donc en équilibre au point d’appui milieu de son levier, le tout étant sur 3ème levier de longueur L2 en équilibre sur le point d’appui au milieu du levier.
x* (1) (2)

(3)

On voit alors que l’immersion dans le second système (à droite) qui ne contenait aucun objet respectivement dans chaque dispositif archimédien en chacun des deux fléaux du levier de deux plus petits objet objets détectables de même volume Vd ne change pas l’équilibre local du système (2) ni celle du système (1) où l’immersion de x* objet indétectable laisse le sous-système (1) en équilibre mais rompt l’équilibre du système global (3) que pour rétablir l’équilibre il faut déplacer le point d’appui (3) vers la droite jusqu’à l’obtenir.
A l’équilibre on en déduit une valeur détectable de Vx* qui était L-DA2-indétectable.
Nous avons encore réussi à rendre 2-L-DA2- détectable un objet qui était L-DA2-indétectable
Le procédé est récursif.
C’est à dire que l’on va se trouver avec des indétectables du 3ème ordre rendus détectables dans un système à 3 étages 3-L-DA2 par duplication du schéma 2-L-DA2 et en mettant les deux sous-systèmes sur un même levier en équilibre sur son point en son milieu .
Nous n’avons toujours pas réussi à isoler la notion de plus petit volume d’eau possible puisque qu’à chaque limitation nous avons trouvé un procédé concret pour aller au delà.
Dire qu’il existe des objets physiques mesurables c’est donc dire qu’il existe aussi des objets physiques mesurables indirectement. Autrement dit ce sont des objets physiques réels qu’on ne peut détecter que par l’accumulation et la comparaison de mesures.
Réciproquement, est-ce qu’à tout ensemble de mesures il correspond un objet physique réel débouche sur la notion d’objet significatifs ou d’objets non significatifs pour ces objets indirects de la physique.
Les objets considérés comme réels de la physique sont donc des classes d’objets. L’objet instancié, i.e. sous la mesure est donc équivalent à une population d’autres objets supposés tous aussi représentatifs de la classe. L’objet mesuré est donc un éléments quelconque de cette classe.
Avant de pouvoir mesurer les objets-phénomènes, il faut être capables de séparer indirectement un phénomène en sous-phénomènes et inversement être capable de voir indirectement plusieurs sous-phénomènes comme constituant un même phénomène.
La séparation est donc une opération abstraite conceptuelle susceptible d’être opérationnalisée dans le terrain concret de la mesure par l’organisation d’une expérimentation en tant qu’instance représentative. Cette opération peut délivrer soit des objets physiques significatifs soit des objets physique non-significatifs.
Réciproquement la synthèse sous la forme d’un même objet physique de mesures multiples issues de l’expérimentation est aussi une opération abstraite susceptible d’être opérationnalisée pouvant de même délivrer un objet physique significatif ou un objet physique non-significatif.
Nous avons donc une double dimension du phénomène physique qui est posé comme un individu quelconque d’une population potentiellement infinie d’objets strictement équivalents et qui est vue aussi d’une manière plus globale comme une classe dont le comportement peut-être résumé par une loi particulière parmi l’ensemble des lois possibles susceptibles de caractériser des classes d’objets.
Il est cohérent, naturellement, que plus un objet acquiert de la précision dans sa mesure (i.e plus il est mesuré significativement par rapport à un (ou plusieurs) critère de mesure) et plus il est non-significatif par rapport aux complémentaires des critères de mesures où il apparaît significatif.
Dans la mesure où on admet que les critères de mesure partitionnent l’espace de toutes les propriétés possibles qu’un objet peut avoir, on comprend aisément que si un objet vérifie une propriété donnée est logiquement équivalent à ce qu’il ne vérifie pas la (ou les ) contraposée de cette propriété.
Donc par définition même des caractéristiques sur un objet, un objet ne peut vérifier positivement toutes les caractéristiques à la fois en même temps mais apparaîtra avec son caractère significatif (sur l’ensemble des caractéristiques où il a des mesures significatives ) et son caractères non-significatif (sur l’ensemble complémentaires des caractères où il a des mesures significatives)
Autrement dit un objet physique aura une image correspondant aux caractères positifs considérés de l’objet et une ombre correspondant aux caractères complémentaires des caractères positifs de l’objets dans l’espace des propriétés possibles .
L’image est plus moins précise et suit le degré de précision des caractères significatifs de l’objet.
L’ombre correspond aux caractères complémentaires ou non-significatifs de l’objet physique .
Autrement dit ce qui est posé en physique est que l’espace des problèmes de la physique est mesurable .
Autrement dit à tout problème physique il existe un objet physique (réel ou virtuel) solution .
C’est à dire pour tout problème, il n’y a pas de problème.
Si une solution en physique est évidemment un objet physique donc mesurable, en revanche un problème physique a un statut plus ambigu dans la mesure où un problème en physique est l’image inverse justement d’une solution physique. Ontologiquement d’ailleurs la solution précède le problème car la solution est toujours mesurable et se hiérarchise naturellement du simple au complexe tandis que le problème est plus hypothétiquement mesurable puisqu’il requiert le concept de solution de solutions c’est à dire de solutions physiques hiérarchiquement structurées. Autrement dit un problème physique suppose une catégorisation de l’espace des solutions physiques d’où donc un concept de solution physique globale peut émerger.
Or la solution est un concept physique ponctuel dans la mesure où est considéré comme objet physique tout objet qui soit justement mesurable c’est à dire comparable à, mis en correspondance avec, un autre objet ou groupe d’objets eux-mêmes objets mesurables.
Cette notion de mesurabilité d’objet doit en outre contenir un principe de finitude, faute de quoi l’objet perd sa singularité d’objet justement et c’est un effet de ponctualité qui vient évidemment du fait que la boucle d’éclatement de l’objet en sous objets doit s’arrêter au bout d’un temps physique fini (le temps de la mesure) sous peine de tomber dans la régression infinie. Le processus de singularisation de l’objet doit admettre une limite inférieure et donc la physique connaît la notion de plus petit objet mesurable.
Les problèmes surgissent bien entendu aux limites et le plus petit objet mesurable est en même temps l’objet le moins mesurable en ce qu’il ne peut se comparer qu’à lui-même.
Les objets physiques qui ne peuvent se comparer qu’à eux-mêmes constituent les objets limites de ce qui peut se considérer comme objets mesurables.
De même que les entiers premiers existent bel et bien en mathématiques et qu’ils sont en nombre infinis, de même ces objets physiques qui ne sont comparables qu’à eux-mêmes existent bel et bien en physique et constituent la base ultime sur laquelle repose la mesurabilité. N’étant comparables qu’à eux-mêmes leurs mesures ne se décomposent pas en mesures d’objets comparables et apparaissent donc comme des objets stochastiques.
On peut tirer de là que pragmatiquement, s’il s’agit de mesurer des objets, l’objet le moins mesurable sera la limite de la mesurabilité des objets et partant, la norme réelle sur laquelle va se baser la fondation de la mesure.
En physique, de façon informelle les objets perçus directement seront mesurable directement en terme d’éloignement par rapport à un objet déclaré limite de la mesurabilité ( ce peut-être le plus petit ou le plus éloigné des objets perçus ) les objets non-perçus directement vont être mesurés indirectement mais exigent un motif de perception qui est une sorte d’entité-objet du second ordre, un objet global de nature graphique. Alors que les objets perçus directement sont comparables uniquement dans des chaînes unidimensionnelles, ces objets seconds sont à la fois dans des chaînes qu’on peut dénommer horizontales traduisant la hiérarchie des objets en tant que singularités et dans des chaînes qu’on peut dénommer verticales traduisant la hiérarchie des objets en tant que constituants d’objets globaux. Ces objets issus de la mesure indirecte ont une nature double, une composante est dûe à leur aspect direct (en tant qu’ils sont un élément particulier d’une famille d’objets perçus) et une seconde composante dûe à leur aspect indirect ( en tant qu’ils sont aussi dans un motif particulier d’objets physique). On peut considérer ces conglomérats d’objets physiques comme une image inverse de groupes constitués d’objets directement perçus.
Moyennant donc la notion de l’existence et de la significabilité de la plus petite solution on évite la redoutable régression à l’infini implicitement contenu dans le principe atomiste, et on peut concevoir sans risque une nouvelle notion de solutions faites à partir d’autres solution de sorte que à quelque niveau que ce soit on ait une mesure d’objet d’un niveau donné compatible avec la mesure des objets de la chaîne des objets dans laquelle il se situe. L’image inverse d’une solution de solutions est évidemment un problème, mais alors que par construction une solution de solutions est rigide donc de nature ponctuelle et finie et appartient irrémédiablement à un monde discret, l’image inverse qui est le problème et qui correspond à la catégorisation des solutions en sous-ensembles de solutions est un élément quelconque de cet ensemble potentiel de solution de solutions possible et donc le problème associé à une solution physique n’est qu’un élément pris dans un ensemble qui a lui la structure du continu. Un autre élément pris au hasard dans ce même ensemble continu est tout aussi représentatif. Alors qu’à une solution il correspond exactement une et seule mesure, à une solution de solutions possible c’est-à-dire à un problème il correspond une classe de mesures possible et en puissance cette classe est infinie.
[Alliot 94] J-M.Alliot., T.Schiex : « Intelligence Artificielle et Informatique Théorique. » Cépaduès, Éditions. 1994. [Belhamissi 89] B. Belhamissi: « Contribution à la cognition des systèmes de représentations pour la résolution des problèmes. ». First Maghrebin Symposium on Software Programming and I.A. Constantine 1989. [Bertalanffy 68] L.V. BERTALANFFY: « Théorie générale des systèmes ». Edition Dunod. 1968. [Chaitin 2000] G.J. CHAITIN: « A century of controversy over the foundations of Mathematics. » in C.Calude and G.Paun, Finite versus Infinite,Springer-Verlag London,2000 pp75-100. [Chaitin 95] G.J. CHAITIN: « Randomness in arithmetic and the decline and fall of reductionismin pure mathematics ». in Nature ‘s Imagination, J.Crornwell, Oxford University Press, 1995. [Chaitin 87] G.J. CHAITIN: « Algorithmic information theory ». Cambridge university press. 1987. [Godefroy,Laubenheimer 2000] G GODEFROY, F.LAUBENHEIMER, Actualités de l’infini« Le zéro et l’infini » SPÉCIAL MATHÉMATIQUES • MAI 2000 CNRS INFO [Davis 83] M.D.DAVIS, E.J.Weyuker: « Computability, complexity and languages. Fundamental of theoretical computer science. » Academic press. 1983. [d’Espagnat 80] B. d’ESPAGNAT: « À la recherche du réel. Le regard d’un physicien. » Gauthiers-Villars. 1980 [Gross 70] M.GROSS, A.LENTIN: « Notions sur les grammaires formelles ». Edition Gauthiers-Villars. 1970. [Hofstader 85] D.R. HOFSTADER: « Gödel, Escher, Bach: les brins d’une guirlande éternelle. ». InterÉdition, Paris. 1985.
Laborit 68] H. LABORIT : « La cybernétique et la machine humaine. ». dans « Le dossier de la cybernétique » Edition Marabout Université. 1968
[Lewis 81]H.R. LEWIS., C.H. Papadimitriou: « Elements of the theory of computation. » Prentice-Hall. 1981. [Penrose 95] R. PENROSE: « Les ombres de l’esprit. À la recherche d’une science de la conscience. ». InterÉdition, Paris. 1995. [Pitrat 92] J. PITRAT : « La symbiose entre l’I.A. et la science cognitive ». T.S.I., vol 11 n°2, pp 9-23. 1992. [Poundstone 85] W. POUNDSTONE: « The recursive universe. Cosmic Complexity and the Limits of Sientific Knowlege. » Oxford university press. 1983.Bibliographie additionnelle
En langue anglaise
1) Introductions
Churchland, P.M. [1984] Matter and Consciousness, Cambridge, M.I.T. Press.
Davies, M. [1995] « The Philosophy of Mind » in A.C. Grayling (dir. publ.) Philosophy, A Guide Through the Subject, Oxford, Oxford U.P., pp. 250-335.
Dennett, D. [1969] Content and Consciousness, Routledge & K.P., Boston.
Guttenplan, S. [1994] (dir. publ.) A Companion to the Philosophy of Mind, B. Blackwell, Cambridge.
Kenny, Anthony [1989] The Metaphysics of Mind, Oxford, Oxford U.P.
Kim, Jaegwon [1996] Philosophy of Mind, Westview Press.
McGinn, Colin [1993] Problems in Philosophy, Cambridge, B. Blackwell.
Rey, G. [1997]
2) Ouvrages collectifs (généraux)
Beakley, B. et al. (dirs publ.) [1992] The Philosophy of Mind, Cambridge, M.I.T. Press.
Block, N. (dir. publ.) [1980] Readings in Philosophy of Psychology (2 vols), Cambridge, M.I.T. Press.
Goldman, A.I. (ed) Readings in Philosophy and Cognitive Science, M.I.T. Press, Cambridge, 1993.
Haugeland, J. (dir. publ.) [1981] Mind Design, Cambridge, M.I.T. Press. (voir la dernière édition [1997].
Kornblith, H. (dir. publ.) [1994] Naturalizing Epistemology, (2nd ed.), Cambridge, M.I.T. Press.
Lycan, W.C. (dir. publ.) [1990] Mind and Cognition: A Reader, Oxford, B. Blackwell.
McDonald, G. and McDonald P. (dirs publ.) Philosophy of psychology, Blackwell, Oxford, 1995.
Rosenthal, D. (dir. publ.) [1968] Materialism and the Mind-Body Problem, Cambridge, Hackett.
Rosenthal, D. (dir. publ.) [1991] The Nature of Mind, Oxford, Oxford University Press.
Stich, S. et al. (dirs publ.) [1991] Philosophy and Connectionist Theory, Hillsdale, Erlbaum.
Warner, R et al. (dirs publ..) [1994] Mind-Body Problem, Oxford, B. Blackwell
3) Quelques ouvrages sur le thème de l’intentionnalité
Cummins, R. [1989] Meaning and Mental Representation, Cambridge, M.I.T. Press
Dennett, D. [1969] Content and Consciousness, RKP.
Dennett, D. [1987] The Intentional Stance, Cambridge, M.I.T. Press.
Fodor, J. [1987] Psychosemantics: The Problem of Meaning in the Philosophy of Mind, Cambridge, M.I.T. Press.
Searle, J. [1983] Intentionnality: an Essay in the philosophy of Mind, Cambridge: Cambridge University Press
Stich, S. et al. (dirs publ.) [1994] Mental Representation, Oxford, B. Backwell.
4) Quelques ouvrages sur le thème de la conscience
Block, N. et al. (dirs publ.) [1997] The Nature of Consciousness, Cambridge, M.I.T. Press.
Chalmers, D. [1996] Toward a Theory of Consciousness, Oxford, Oxford U. Press.
Davies, M. et al. (dirs publ.) [1993] Consciousness: Psychological and Philosophical Essays, Oxford.
Dretske, F. [1996] Naturalizing the Mind, Cambridge, M.I.T. Press.
Flanagan, O. [1992] Consciousness reconsidered, Cambridge, M.I.T. Press.
Lycan, B. [1996] Consciousness and Experience, Cambridge, M.I.T. Press.
McGinn, C. [1991] The Problem of Consciousness, Oxford, B. Blackwell.
Searle, J. [1992] The Rediscovery of the Mind, Cambridge, M.I.T. Press.
Tye, M. [1995] Ten Problems of Consciousness, Cambridge, M.I.T. Press.
5) Quelques classiques
Churchland, P.M. [1995] The Engine of Reason, the Seat of the Soul: a Philosophical Journey into the Brain, Cambridge, M.I.T. Press.
Churchland, P.M. [1979] Scientific Realism and the Plasticity of Mind, Cambridge, Cambridge U.P.
Davidson, D. [1980] Essays on Actions and Events, Oxford, Oxford U.P.
Davidson, D. [1984] Inquiries into Truth and Interpretation, Oxford, Oxford U.P.
Dennett, D. [1969] Content and Consciousness, RKP.
Dennett, D. [1984] Elbow Room: The Varieties of Free Will worth wanting, Cambridge, M.I.T. Press.
Dennett, D. [1978] Brainstorms: Philosophical Essays on Mind and Psychology, Cambridge, M.I.T. Press.
Dennett, D. [1987] The Intentional Stance, Cambridge, M.I.T. Press.
Dennett, D. [1991] Consciousness Explained, Boston, Little Brown.
Dennett, D. [1996] Kinds of Mind: Towards an Understanding of Consciousness, New York, Basic Books.
Dretske, F. [1988] Explaining Behavior: Reasons in a world of Causes, Cambridge, M.I.T. Press.
Dretske, F. [1995] Naturalizing the Mind, Cambridge, M.I.T. Press.
Fodor, J. [1975] The Language of Thought, Harvard, Harvard U.P.
Fodor, J. [1987] Psychosemantics: The Problem of Meaning in the Philosophy of Mind, Cambridge, M.I.T. Press.
Nagel, T. [1979] Mortal Questions, Cambridge, Cambridge University Press
Putnam, H. [1981] Reason, Truth and History, Cambridge, Cambridge University Press
Putnam, H. [1988], Representation and Reality, Cambridge, M.I.T. Press.
Putnam, H. [1975] Mind, Language and Reality (Philosophical Papers vol. 2), Cambridge, Cambridge U.P.
Searle, J. [1983] Intentionnality: an Essay in the philosophy of Mind, (Cambridge),
Searle, J. [1984] Minds, Brains and Science, Cambridge, Harvard U.P.
Searle, J. [1992] The Rediscovery of the Mind, Cambridge, Cambridge U.P.
Sellars, W. [1963] « Empiricism and the philosophy of Mindî, Science, Perception and Reality, RKP.
Stich, S. [1983] From Folk Psychology to Cognitive Science, Cambridge, M.I.T. Press.
B) En langue française
6) Les classiques (en traduction française)
Cayla, F. (dir. publ.) [1991] Routes et déroutes de l’intentionnalité: la correspondance W. Sellars/R. Chisholm, Combas, Öclat.
Davidson, D. [1980] Actions et événements, trad. franç. par P. Engel, Paris, P.U.F. 1993.
Davidson, D. [1991] Paradoxes de l’irrationnalité, trad. franç. par P. Engel, Combas, Éclat.
Dennett, D. [1987] La stratégie de l’interprète: le sens commun et l’univers quotidien, trad. franç. par P. Engel, Paris, Gallimard, 1990.
Dennett, D. [1991] La conscience expliquée, trad. franç. par P. Engel, Paris, O. Jacob, 1993.
Nagel, T.[1979] Questions mortelles, trad. franç. P. Engel, Paris, P.U.F., 1983.
Putnam, H. [1981] Reason, Truth and History (Cambridge), trad. franç. par A. Gerschenfeld, Raison, vérité et histoire, Paris, Minuit, 1984.
Putnam, H. [1988], Representation and Reality, Représentation et réalité, trad. franç. par C. Tiercelin, Paris, Gallimard, 1990.
Ryle, G. [1949] The Concept of Mind, trad. franç. par S. Stren-Gillet, La notion d’esprit, Paris, Payot, 1978.
Searle, J. [1983] Intentionnality: an Essay in the philosophy of Mind, (Cambridge), trad. franç. par C. Pichevin, L’intentionnalité: Essai de philosophie des états mentaux, Paris, Minuit, 1985.
Searle, J. [1984] Du cerveau au savoir, trad. franç. par C. Chaleyssin, Paris, Hermann, 1985.
Searle, J. [1992] The Rediscovery of the Mind, Cambridge, Cambridge U.P.
Sellars, W. [1963] Empirisme et philosophie de l’esprit, Combas, l’Éclat, 1992.
7) Ouvrages collectifs en français
Anderson, A.R. (dir. publ.) [1964] Pensée et machine, trad. franç. P. Blanchard, Paris, Champ Vallon, 1983.
Andler, D. et al. (éds.) [1992] Épistémologie et cognition, Liège, Mardaga.
Andler, D. (éd.) [1992] Introduction aux sciences cognitives, Paris, Gallimard.
Hofstadter, D.R. et al. (dirs publ.) [1981] Vues de l’esprit, trad. franç. de J. Henry, Paris, Interéditions, 1987.
Engel, P. (éd.) [1984] Lire Davidson, Combas, L’éclat.
Fisette, D. (éd.) [1992] D. Dennett et les stratégies intentionnelles, Lekton vol 2, no. 1.
Fisette, D. et al. (dirs publ.) [1996] Penser l’esprit: des sciences de la cognition à la philosophie cognitive, Grenoble, Presses universitaires de Grenoble.
Hofstadter, D.R. et al. (dirs publ.) [1981] Vues de l’esprit, trad. franç. de J. Henry, Paris, Interéditions, 1987.
8) Commentaires et ouvrages généraux en français
Descombes, V. [1996] Les institutions du sens, Paris, Minuit.
Dreyfus, H. [1979] Intelligence artificielle: mythes et limites, trad. franç. par R.-M. Vassao, Paris, Flammarion, 1984.
Dupuy, J.-P. [1994] Aux origines des sciences cognitives, Paris, La découverte.
Engel, P. [1994] Introduction à la philosophie de l’esprit, Paris, La découverte.
Engel, P. [1996] Philosophie et Psychologie, Paris, Gallimard, 1996.
Haugeland, J. [1985] L’esprit dans la machine, trad. franç. J. Henry, Paris, O. Jacob, 1989.
Jacob, P. [1992] « Le problème du rapport du corps et de l’esprit aujourd’hui » in D. Andler [1992], p. 313-351.
Pacherie, E. [1993] Naturaliser l’intentionnalité, Paris, P.U.F.
Varela, F. [1996] Invitation aux sciences cognitives, Paris, Seuil.
Varela, F. et al. [1993] L’inscription corporelle de l’esprit: sciences cognitives et expérience humaine, Paris, Seuil, 1993.
Winograd, T. et Flores, F. [1986] L’intelligence artificielle en question, trad. franç. J.-L. Peytavin, Paris, P.U.F. 1989.
Biblio additionnelle
Bell, E. T. « Paradise Lost: Cantor. » Ch. 29 in Men of Mathematics: The Lives and Achievements of the Great Mathematicians from Zeno to Poincaré. New York: Simon and Schuster, pp. 555-579, 1986.
Dauben, J. W. Georg Cantor: His Mathematics and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1990.
Quelques ouvrages disponibles sur le web dont certains en ligne:
LES FONDEMENTS DES MATHÉMATIQUES, Dr F. Gonseth, Libraire scientifique et technique A. Blanchard
Paris – 1926/1974 – De la géométrie d’Euclide à la relativité générale et à l’intuitionnisme
ABRÉGÉ D’HISTOIRE DES MATHÉMATIQUES, 1700-1900, Jean Dieudonné et une équipe de mathématiciens. Ch X1, Axiomatique et logique par Marcel Guillaume, Ed. Hermann, Paris – 1978
Les principes fondamentaux de la géométrie par David Hilbert :
http://archive.numdam.org/ARCHIVE/ASENS/ASENS_1900_3_17_/ASENS_1900_3_17__103_0…pdf
La théorie des invariants au 19è siècle par Jean Dieudonné (séminaire Bourbaki (1970-71) sur le site Numdam :
http://archive.numdam.org/ARCHIVE/SB/SB_1970-1971__13_/SB_1970-1971__13__257_0/SB_…pdf
Intégration & Analyse hilbertienne, A. Guichardet , Éd. Ellipses X École polytechnique, Paris, 1989
.
Analyse fonctionnelle, espaces de Hilbert, dualité, théorie spectrale par Claude Portenier, univ. Marburg :
http://www.mathematik.uni-marburg.de/~portenier/Analyse-fonctionnelle/af-tot.pdf
La géométrie de Hilbert, étude de Fabien Besnard :
http://perso.wanadoo.fr/fabien.besnard/vulg/tout/les axiomes de hilbert.html
Le formalisme à travers la géométrie, par Jean Merker (Univ. Franche-Comté,1983) :
http://epiphymaths.univ-fcomte.fr/Merker-Formalisme_a_travers_la_geometrie.pdf
Espaces de Hilbert et séries de Fourier, cours de Charles Suquet (Univ. de Lille) :
http://math.univ-lille1.fr/~suquet/ens/IFP/Cours/cours04/Chap7ifp04.pdf
Théorie des équations intégrales linéaires (en allemand), sur le site Internet Archive :
https://archive.org/stream/grundzugeallg00hilbrich#page/n7/mode/2up
Théorie des invariants (en français), on pourra consulter Hilbert et la notion d’existence en mathématiques sur Google Livres :
http://books.google.fr/books?id=yBJ_5EvM0q8C&pg (aller à la page 53).
Theory of algebraic invariants, par David Hilbert (1897), édition en anglais (2008) :
http://www.amazon.de/Algebraic-Invariants-Cambridge-Mathematical-Library/dp/0521449030
Problèmes de Hilbert sur le site de D. E. Joyce : http://aleph0.clarku.edu/~djoyce/hilbert/toc.html
Le Zahlbericht (en anglais), édition limitée sur Google Livres:
http://books.google.fr/books?id=_Q2h83Bm94cC&printsec=frontcover&hl=fr#v=onepage&q&f=false
Éléments de mathématiques, Livre V – Nicolas Bourbaki
Espace vectoriels topologiques, Livre V, Ch. 5: Espace hilbertiens